Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews - Страница 9

При этом среднюю абсолютную ошибку по модулю находят по формуле (2.20):

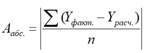
Для нашего уравнения регрессии средняя абсолютная ошибка по модулю по данной формуле была рассчитана таким образом:

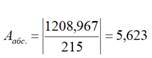
Иначе говоря, прогноз по данной статистической модели в среднем по каждому наблюдению отклонялся от фактического значения курса доллара на 5 руб. 62,3 коп. по модулю.

Среднюю относительную ошибку по модулю в процентах вычисляют по формуле (2.21):

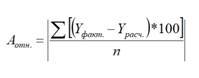
При этом средняя относительная ошибка по модулю в процентах находится в нашем случае таким образом:

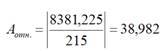
Следовательно, прогноз по данной статистической модели в среднем по каждому наблюдению отклонялся от фактического значения курса доллара на 38,98 %. В то время как о хорошем качестве уравнения регрессии можно говорить лишь в том случае, если средняя относительная ошибка по модулю составит не более 5-7%. (См. учебник «Эконометрика» под ред. И.И. Елисеевой. ‑ 2-е изд., пер. и доп. ‑ М,: Финансы и статистика, 2006, стр. 107).

Для того чтобы окончательно убедиться в непригодности для прогноза данного уравнения регрессии, построим таблицу 2.6, в которой дадим прогнозы и фактический курс доллара за период с января 2009 г. по апрель 2010 г.

Таблица 2.6. Прогноз, фактический курс доллара и остатки с января 2009 г. по апрель 2010 г.

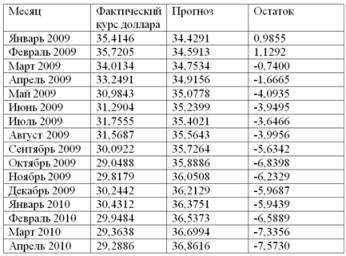
Судя по табл. 2.6, с января 2009 г. по апрелю 2010 г. отклонения от прогноза (остатки), сделанного по уравнению регрессии Y расч.=0,1622*215++ 1,9958, колебались в диапазоне от 98,5 коп. до 7 руб. 57,3 коп., что свидетельствует о невысокой точности данной прогностической модели. Более того, если построить график остатков по линейной прогностической модели, то легко обнаружить, что на нем наблюдается несколько локальных трендов (см. рис. 2.2). А это признак – как мы об этом уже говорили – нестационарности полученных остатков.

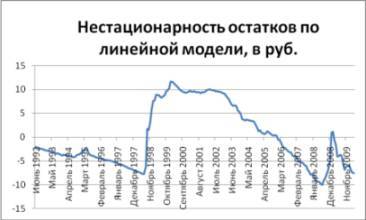
Рис. 2.2. Нестационарность остатков, полученных в линейной статистической модели

Источник: по данным Банка России

Попробуем повысить точность нашего прогноза, используя алгоритм действий № 1 «Как строить диаграммы в Microsoft Excel». С этой целью обведем с помощью мышки столбец с ежемесячными данными (на конец месяца) по курсу пары рубль – доллар за период с июня 1992 г. по апрель 2010 г. и столбец с соответствующими обозначениями месяцев. Выбрав опцию График, строим соответствующую диаграмму, а затем щелкаем с помощью мышки по линии графика и выбираем в появившемся окне опцию ДОБАВИТЬ ЛИНИЮ ТРЕНДА (см. рис. 2.3).

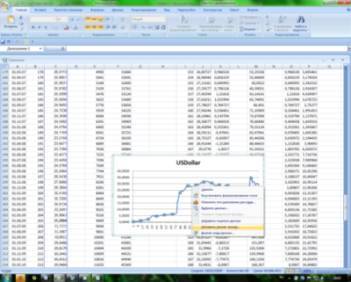
Рис. 2.3. Построение линии тренда на основе графика динамики курса доллара

Далее появляется мини-окно ФОРМАТ ЛИНИИ ТРЕНДА, в котором мы можем выбрать соответствующие ПАРАМЕТРЫ ЛИНИИ ТРЕНДА (рис. 2.3), необходимые для построения прогностических моделей. При этом воспользуемся всеми имеющимися в Excel форматами тренда за одним единственным исключением: из полиномиальных трендов возьмем тренды не выше третьей степени. В научной литературе обычно не рекомендуют использовать для аппроксимации фактических данных более сложные полиномы, поскольку они плохо поддаются интерпретации и ‑ несмотря на высокий коэффициент детерминации (по включенной в статистическую модель базе данных) ‑ обладают низкой прогностической ценностью.

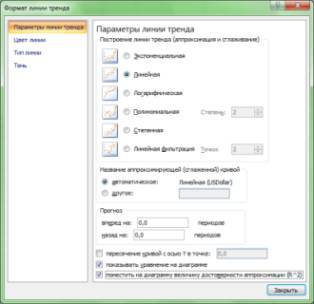
Рис. 2.4. Определение характера и параметров линии тренда

Сначала построим самый простой линейный тренд. С этой целью выберем в мини-окне ФОРМАТ ЛИНИИ ТРЕНДА в опции ПАРАМЕТРЫ ЛИНИИ ТРЕНДА формат тренда ‑ ЛИНЕЙНАЯ. При этом поставим галочку в опциях ПОКАЗЫВАТЬ УРАВНЕНИЕ НА ДИАГРАМММЕ, ПОМЕСТИТЬ НА ДИАГРАММУ ВЕЛИЧИНУ ДОСТОВЕРНОСТИ АППРОКСИМАЦИИ (R^2). В результате получим диаграмму на рис. 2.5, показывающую линейный тренд, то есть линейную зависимость роста курса доллара от времени (от порядкового номера месяца, при июне 1992 год =1).

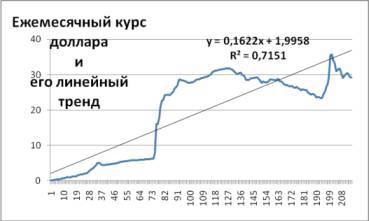
Рис. 2.5. Ежемесячный курс доллара и его тренд: по оси абсцисс вместо названий месяцев даны их порядковые номера (июнь 1992 г. =1, июль 1992 г. =2 … апрель 2010 г. =215)

Поочередно, задавая различные параметры тренда и сравнивая коэффициенты детерминации, составим таблицу 2.7, в которой разместим – по мере роста коэффициента детерминации ‑ прогностические модели с различным форматом тренда. Причем, наиболее высокий коэффициент детерминации у нас получился у уравнения регрессии, полученного путем аппроксимации по степенному тренду. В этом случае R² оказался равен 0,919136, то есть данное уравнение регрессии объясняет 91,91 % всех ежемесячных колебаний курса доллара. Соответственно, доля случайной компоненты оказалась равна = 100% -91,91 %=8,09%.

Для того чтобы правильно интерпретировать уравнения регрессии, полученные графическим способом, необходимо иметь в виду, что в процессе построения тренда программа Excel автоматически задает в качестве зависимой переменной y – ежемесячный курс доллара, а в качестве независимой х – порядковый номер месяца. Например, экономическая интерпретация уравнения регрессии со степенной функцией y = 0,0443609x1,2807295 следующая: курс доллара в период с июня 1992 г. по апрель 2010 г. ежемесячно рос со средней скоростью 28,07 % при исходном уровне 4,44 коп.

Таблица 2.7 «Параметры тренда и величина коэффициента детерминации R2»

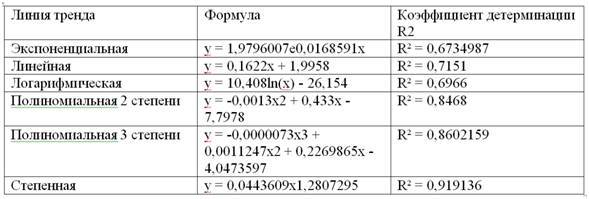
Как мы уже убедились, графический способ решения уравнения регрессии в программе Excel позволяет довольно существенно экономить время. Однако у этого способа есть и один весьма существенный недостаток, обусловленный тем, что в данном случае не проводится оценка статистической значимости, как в целом уравнения регрессии, так и его коэффициентов.

Таким образом, графический способ решения уравнения регрессии целесообразно использовать на этапе предварительного отбора уравнений регрессии, имеющих наиболее высокий коэффициент детерминации. После отбора уравнения регрессии с высоким коэффициентом детерминации, в Excel его нужно решить, используя в Пакете анализа опцию РЕГРЕССИЯ – см. алгоритм действий № 3. Однако решение уравнение регрессии, аппроксимирующего фактические данные степенным трендом, имеет определенную специфику. В отличие от линейного тренда уравнение регрессии решается не относительно имеющихся исходных данных, а по отношению к их логарифмам. Объясняется это тем, что уравнение регрессии со степенным трендом относится по оцениваемым параметрам к нелинейным моделям, но его можно привести к линейному виду.