Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews - Страница 10

В результате уравнение регрессии для степенного тренда (см. табл. 2.7) приобретет следующий вид (2.22):

Следует иметь в виду, что приведение нелинейной функции к линейному виду с помощью логарифмирования используется очень часто, хотя это и приводит к некоторым коллизиям. Вот что пишут по этому поводу Е. М. Четыркин и И.Л. Калихман: «Однако такое преобразование приводит к тому, что оценка параметров базируется не на минимизации суммы квадратов отклонений, а на минимизации суммы квадратов отклонений в логарифмах. …Следствием этого является некоторое смещение оценок параметров, получаемых обычным (линейным) МНК». (см. Четыркин Е. М., Калихман И.Л. Вероятность и статистика. – М.: Финансы и статистика, 1982, стр. 255).

Далее параметры этого уравнения регрессии находятся согласно формулам (2.1.4) и (2.1.5), либо решаются с помощью соответствующей компьютерной программы.

Поэтому прежде чем приступить к выполнению алгоритма действий № 3 «Как решить уравнение регрессии в Excel», нужно взять натуральные логарифмы (логарифмы, основанием которых служит число e= 2,71828), как от независимой переменной х – порядковый номер месяца, так и от зависимой переменной у – курс доллара. В Excel для этих целей можно воспользоваться функцией LN. Далее поступаем в полном соответствии с алгоритмом действий № 3, а данные, полученные после решения уравнения регрессии, занесем в таблицу 2.8.

Таблица 2.8. ВЫВОД ИТОГОВ уравнения регрессии, полученного после логарифмирования исходных данных

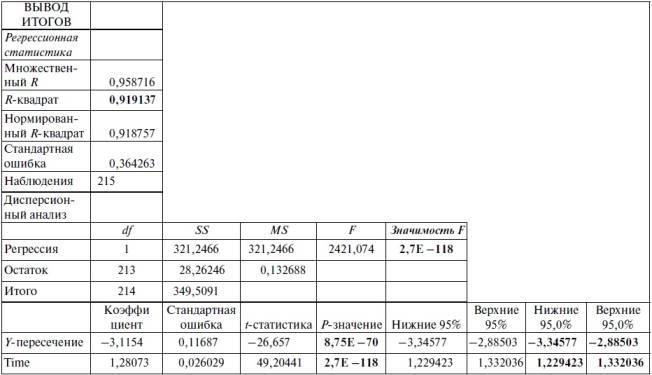
Согласно алгоритму действий № 4 «Оценка статистической значимости уравнения регрессии и его коэффициентов», проведем проверку статистической значимости данного уравнения регрессии. При этом выделим в таблице 2.8 все важнейшие пункты жирным шрифтом. В результате мы пришли к выводу, что у нас получилось статистически значимым как уравнение регрессии, так и его коэффициенты, как при 95% , так и 99% уровнях надежностях. Правда, поскольку данное уравнение регрессии мы решили относительно натуральных логарифмов, взятых от исходных данных, то в результате оно приобрело следующий вид:

Ln Y=-3,1154+1,28073 lnX

Согласно последнему уравнению регрессии, прогноз курса доллара рассчитывается на основе логарифмов, взятых от исходных данных. Например, прогноз относительно апреля 2010 г. вычисляется следующим образом:

Ln Y=-3,1154+1,28073* 5,370638= 3,762939; где 5,370638=ln(215) – натуральному логарифму от порядкового номера апреля 2010 г. =215.

Отсюда находим (в Excel потенцирование натуральных логарифмов производится с помощью функции EXP), прогноз курса доллара на апрель 2010 равен:

Y=EXP(3,762939)= 43,07482

После проведения соответствующих преобразований, вышеуказанное уравнение регрессии приобретет следующий вид:

Y=EXP(-3,1154 + 1,28073 lnX)= 0,044361*X^1,28073

С помощью последнего уравнения регрессии можно делать расчет прогнозов непосредственно от исходных данных, а не от их натуральных логарифмов. В результате прогноз курса на доллара на апрель 2010 г. можно вычислить следующим образом:

Y=0,044361*215^1,28073; где 215 – порядковый номер апреля 2010 г. (при июне 1992 г. =1).

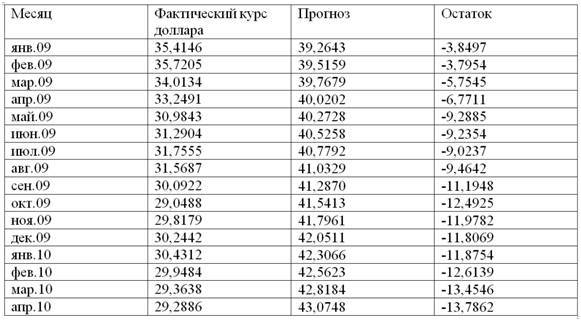
Несмотря на то, что коэффициент детерминации у степенного уравнения регрессии выше, чем у линейного, однако, например, относительно апреля 2010 г. прогноз по данному уравнению регрессии весьма сильно отклоняется от фактического курса доллара, как впрочем, и во многих других случаях. Судя по таблице 2.9, с января 2009 г. по апреля 2010 г. отклонения от прогноза (остатки), сделанного по уравнению регрессии yрасч.= 0,044361*X^1,28073, колебались в диапазоне от -3,7954 руб. до -13,7862 руб., что свидетельствует о невысокой точности данной прогностической модели.

Таблица 2.9. Прогноз по степенному уравнению регрессии, фактический курс доллара и остатки с января 2009 г. по апрель 2010 г.

При этом средняя абсолютная ошибка прогноза по модулю для степенной статистической модели – см. формулу (2.20) – оказалась равна 5 рублям 92, 4 копейкам. Следовательно, этот показатель у данной модели оказался на 30 коп. выше, чем у линейной модели. В свою очередь, средняя относительная ошибка по модулю в процентах ‑ см. формулу (2.21) – для степенной модели оказалась равна 31,10 процентам, то есть на 7,78 процентных пункта ниже, чем у линейной модели. Более того, если построить график остатков по степенной прогностической модели (см. рис. 2.3), то легко обнаружить, что на нем наблюдается несколько локальных трендов. А это – как мы говорили ранее – наглядно свидетельствует о нестационарности остатков.

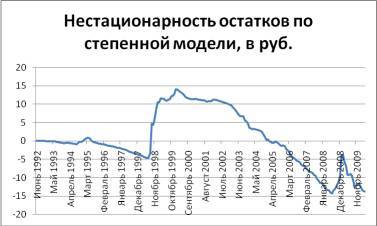
Рис. 2.6. Нестационарность остатков, полученных по степенной прогностической модели

Отсюда можно сделать вывод, что не только линейная модель, но и степенная модель, в которой в качестве независимой переменной использовался фактор времени (порядковый номер месяца), оказались непригодны для прогнозирования курса доллара. Все это заставляет нас продолжить поиск адекватной прогностической модели.

1. В чем суть метода наименьших квадратов, как этот метод можно представить графически?

2. Перечислите все пункты алгоритма действий, которые необходимо выполнить при решении уравнения регрессии в Microsoft Excel.

3. Какое уравнение регрессии (при прочих равных условиях) точнее: то, которое имеет коэффициент детерминации (R-квадрат)=0,757, либо то, у которого (R-квадрат) равен 0,978. Объясните почему?

4. Скажите, можно ли признать статистически значимым уравнение регрессии в том случае если значимость его F-критерия =009? И если можно, то с каким уровнем надежности?

5. В каком случае делается вывод о статистической значимости коэффициентов уравнения регрессии? Скажите, при каком Р-значении коэффициенты уравнения регрессии являются статистически значимыми с 95% уровнем надежности и с 99% уровнем надежности?

6. Перечислите формат трендов, используемых в Excel при решении уравнений регрессии графическим способом. Чем эти форматы трендов отличаются друг от друга.

Глава 3.

Уравнения авторегрессии и авторегрессии со скользящим средним

В главе 2 мы убедились, что использование фактора времени для прогноза курса доллара не дает достаточно точного результата. Поэтому необходимо найти более подходящую независимую переменную (или переменные). Как известно, согласно теории эффективного рынка, наиболее полную информацию для прогноза будущей стоимости какого-либо финансового актива в момент времени t можно извлечь из его цены в момент времени t-1. Причем, точность прогноза уменьшается по мере того как прогноз делается в моменты времени t-2, t-3 … и т.д. Исходя из этого вполне очевидного постулата, можно прийти к выводу, что наиболее полную информацию о курсе доллара на момент времени t содержит его курс на момент времени t-1. Следовательно, наиболее точный прогноз курса американской валюты можно рассчитать на основе уравнения регрессии, включив в него в качестве независимой переменной курс доллара с лагом t-1. Такого рода уравнения регрессии, в которых значения результативного признака прогнозируются на основе его предыдущих значений, в статистической литературе называют уравнениями авторегрессии.