Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews - Страница 11

Правда, в отличие от прогностической модели, в которой в качестве независимой переменной используется фактор времени, а потому горизонт для прогноза практически безграничен, прогноз по авторегрессионной модели имеет небольшой временной горизонт для прогноза, равный длине лага. В частности, модель авторегрессии с лагом в один месяц способна давать прогноз с упреждением в один месяц.

Помимо относительно небольшого временного горизонта для прогноза, в процессе построения моделей авторегрессии возникают еще одна серьезная проблема. Дело в том, что наличие лаговых значений зависимой переменной в правой части уравнения приводит к нарушению одной из важнейших предпосылок метода наименьших квадратов (МНК) об отсутствии связи между зависимой (результативной) и независимой (факторной) переменной. Математически эта проблема может быть изложена следующим образом – см. формулу (3.1):

Где: с – свободный член (константа) уравнения, Yt – зависимая (результативная) переменная, Y t-1 – независимая (факторная) переменная с лагом в один месяц, b – соответствующий коэффициент при Y t-1, et – отклонение прогноза от фактического курса доллара (остаток) в текущем месяце t.

Таким образом из формулы (3.1) следует, что в уравнении авторегрессии может иметь место: во-первых, зависимость между et и e t-1, то есть может быть нарушена предпосылка МНК об отсутствии автокорреляция в остатках; во-вторых, может появиться зависимость между факторной переменной Y t-1 и остатками et, то есть будет нарушена предпосылка МНК о гомоскедастичности остатков.

Наличие автокорреляции в остатках означает определенную связь (корреляцию) между остатками текущих и предыдущих наблюдений. При наличии такой зависимости остатки могут, либо содержат определенную тенденцию, либо какие-то циклические колебания. В этом случае делается вывод, что отклонения от прогноза не носят случайный характер. При наличии автокорреляции в остатках оценки коэффициентов уравнения регрессии нельзя назвать состоятельными и эффективными.

Гомоскедастичность остатков означает, что дисперсия остатков Et не изменяется в зависимости от величины факторной переменной Yt-1. Если это не так, то возникает гетероскедастичность остатков, что также ‑ как и в случае автокорреляции в остатках ‑ влияет на состоятельность оценки коэффициентов уравнения регрессии.

Для справки заметим, что состоятельными оценками называются такие оценки, чья точность повышается по мере роста объема выборки, объема данных, на основе которых строится уравнение регрессии. В свою очередь, эффективными оценками называются такие оценки, которые имеют наименьшую дисперсию.

Несмотря на вышеуказанные опасения, многие авторитетные специалисты полагают, что в случае больших выборок уравнения авторегрессии позволяют получать состоятельные и эффективные оценки. Вот как, например, оценивает авторегрессионные модели профессор статистики Стэнфордского университета Т. Андерсон: «Модель авторегрессии обладает рядом преимуществ по сравнению с моделью скользящего среднего и процессом авторегрессии с остатками в виде скользящего среднего, хотя последние в определенных случаях могут хорошо описывать образование наблюдаемых временных рядов. Оценки коэффициентов процесса авторегрессии легко вычисляются. Статистические процедуры для такого процесса, основывающиеся на теории больших выборок, легко выполнимы, поскольку они соответствуют обычной технике наименьших квадратов. Во многих случаях коэффициенты процесса авторегрессии допускают непосредственную интерпретацию, а линейные функции от запаздывающих переменных могут быть использованы для прогнозирования (см. Т. Андерсон. Статистический анализ временных рядов. Пер. под ред. Ю.К. Беляева. Издательство «Мир», М., 1976 стр. 276).

Следует заметить, что в зависимости от того, сколько предыдущих значений временного ряда будет включено в уравнение авторегрессии в качестве лаговых (факторных) переменных, принято различать авторегрессионный процесс разного порядка. Так, в формуле 3.1. представлен авторегрессионный процесс первого порядка, который в англоязычной литературе обычно называется словосочетанием Auto Regressive и кратко обозначается как AR(1).

В том случае, когда в авторегрессию первого порядка добавляются лаговые переменные Yt-2 и Yt-3, то его принято обозначать как AR(3), то есть как авторегрессионный процесс третьего порядка. При этом уравнение для AR(3) примет вид (3.2):

где Y t-1, Y t-2 и Y t-3– независимые (факторные) переменные с лагом в один, два и три месяц; b1,b2 и b3 – соответствующие коэффициенты регрессии при лаговых переменных.

Помимо авторегрессионных моделей, нам необходимо также познакомиться и с моделями со скользящим средним в остатках, которые в англоязычной литературе обычно называется словосочетанием Moving Average. Полезность моделей со скользящим средним в остатках обусловлена тем, что для стационарного ряда предсказываемую переменную Yt можно представить в виде линейной функции прошлых ошибок (отклонений прогнозов от их фактических значений). Следует иметь в виду, что термин «скользящая средняя» в данном случае не является синонимом скользящей средней, применяемой, например, для сезонного сглаживания уровней динамического ряда. При этом модель со скользящими средними в остатках первого порядка кратко обозначается как МА(1), а ее формула имеет следующий вид:

Объединение в одной модели авторегрессионного процесса AR и модели со скользящим средним в остатках МА приводит к созданию более экономичной модели с точки зрения количества используемых параметров. Эту объединенную модель в англоязычной литературе кратко называют ARMA. Данная аббревиатура произошла от словосочетания ‑ Auto Regressive ‑ Moving Average, что в переводе означает авторегрессионный процесс со скользящими средними в остатках.

Порядок в этой модели в буквенной форме принято обозначать как ARMA(p,q), где p ‑ величина порядка авторегрессионного процесса, а q – величина порядка процесса со скользящим средним в остатках. Например, модель ARMA (2;1) фактически представляет собой комбинацию модели AR (2) с моделью MA(1), то есть в одной модели объединена авторегрессионная модель второго порядка с моделью со скользящим средним в остатках первого порядка. В результате модель ARMA (2;1) приобретает вид (3.4):

Для того, чтобы объединенная модель ARMA(2;1) была нашим читателям более понятна, ее можно задать в виде двух уравнений. Так, для AR(2) формула будет иметь вид (3.5)

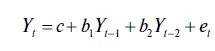
В то время как уравнения для MA(1) можно представить так (3.6):

Следовательно, формулу (3.4) модели ARMA(2; 1) можно получить путем вычитания из

левой части формулы (3.5) левой части уравнения (3.6).