Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews - Страница 8

В данном случае для свободного члена уравнения эта функция приобретает следующий вид: СТЬЮДРАСП (2,284573;215-1-1=213;2)= 0,023323

Следовательно, Р-значение коэффициента свободного члена уравнения показывает, что данный коэффициент значим лишь при 5% уровне значимости, но не значим при 1% уровне значимости.

Для коэффициента регрессии Р-значение в Excel находится следующим образом: СТЬЮДРАСП (23,12267;215-1-1=213;2)= 5,4E-60=0,0

Следовательно, Р-значение коэффициента регрессии показывает, что данный коэффициент значим не только при 5% уровне значимости, но и при 1% уровне значимости.

5. Столбцы Нижние 95% и Верхние 95% показывают соответственно нижние и верхние интервалы значений коэффициентов при 95 % уровне значимости. Для расчета доверительных интервалов сначала находится критическое значение t-критерия, которое в Excel находится с помощью функции СТЬЮДРАСПОБР (α =0,05 ;df=n-k-1); где в опции α – величина риска, коэффициент регрессии (или свободный член) не окажутся в рамках установленных доверительных интервалов); в опции df – число степеней свободы.

Таким образом для 95% уровня надежности t-критерий = СТЬЮДРАСПОБР (α =0,05 ;df=215-1-1)= 1,9712

Далее для свободного члена уравнения находим:

Значение столбца Нижние 95%=Коэффициент – Стандартная ошибка* t-критерий=1,995805– (0,873601*1,9712)= 0,273794.

Значение столбца ВЕРХНИЕ 95%=Коэффициент + Стандартная ошибка* t-критерий=1,995805 + (0,873601*1,9712)= 3,717815.

Для коэффициента регрессии Time находим:

Значение столбца Нижние 95%=Коэффициент – Стандартная ошибка* t-критерий=0,162166– (0,007013*1,9712)= 0,148342.

Значение столбца ВЕРХНИЕ 95%=Коэффициент + Стандартная ошибка* t-критерий=0,162166+ (0,007013*1,9712)= 0,175991.

6. Столбцы Нижние 99% и Верхние 99% показывают соответственно нижние и верхние интервалы значений коэффициентов при 99 % уровне значимости. При этом значения столбца Нижние 99% и Верхние 99% находятся аналогичным образом, как и значения столбцов Нижние 95% и Верхние 95%.

Единственное отличие, это расчет t-критерия для 99% уровня надежности. При этом t-критерий = СТЬЮДРАСПОБР (α =0,01 ;df=215-1-1)= 3,3368. Найденный t-критерий используют при нахождении 99% доверительных интервалов для свободного члена и коэффициента регрессии. Правда, с коэффициентом свободного члена у нас возникает довольно серьезная проблема. Дело в том, что при 99% уровне надежности у коэффициента свободного члена при переходе от столбца Нижние 99% к столбцу Верхние 99% происходит смена знака от минуса к плюсу. Вполне очевидно, что в практических расчетах столь неоднозначно изменяющийся коэффициент уравнения (он может быть как положительным, так и отрицательным, также равным 0) невозможно использовать. Поэтому для 99 % уровня надежности коэффициент свободного члена уравнения считается статистически незначимым, в то время как для 95 % уровня надежности данный коэффициент считается статистически значимым, поскольку в последнем случае при переходе от столбца Нижние 95% к столбцу Верхние 95% смена знака происходит от минуса к плюсу

Алгоритм действий № 4 «Оценка статистической значимости уравнения регрессии и его коэффициентов»

Суммируя вышесказанное, приведем краткий алгоритм принятия решения о статистической значимости уравнения регрессии на основе ВЫВОДА ИТОГОВ в Excel.

Шаг 1. Принятие решения о значимости уравнения регрессии

1.1 Чем ближе R-квадрат к 1, тем лучше, что дает отличный критерий для выбора одного из нескольких уравнений регрессии.

Значимость F должна быть меньше 0,05 – при 95% уровне надежности; при 99% должна быть меньше 0,01 ‑ при 99% уровне надежности уровне.

Шаг 2. Принятие решения о значимости коэффициентов уравнения регрессии

P-Значение должно быть меньше 0,05 – при 95% уровне надежности; при 99% P-Значение должно быть меньше 0,01 ‑ при 99% уровне надежности уровне.

Коэффициенты регрессии и свободного члена при переходе от столбца Нижние и Верхние (при заданном уровне надежности) не должны менять свой знак. Если смена знака происходит, то коэффициенты данного уравнения признаются статистически незначимыми.

Исходя из этого краткого алгоритма, мы отметили жирным шрифтом в ВЫВОДЕ ИТОГОВ (см. табл. 2.5) именно те пункты, на которые следует обратить внимание. При этом те пункты, которые не являются статистически значимыми при данном уровне надежности, мы не только выделили жирным шрифтом, но еще и подчеркнули.

Таблица 2.5. ВЫВОД ИТОГОВ и принятие решения о статистической значимости уравнения регрессии и значимости его коэффициентов

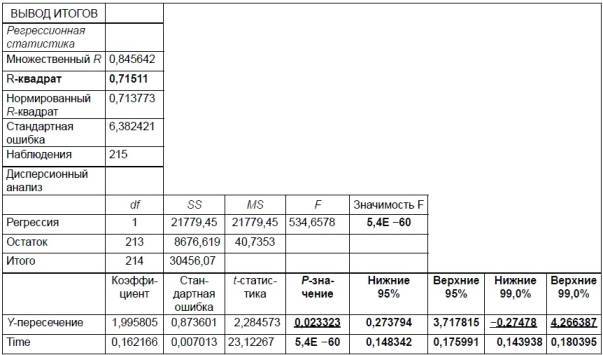
Таким образом, взяв за основу данные из таблицы 2.5 и действуя по алгоритму № 4, мы дадим ответы на все четыре пункта последнего:

1.1. Поскольку коэффициент детерминации R2 для данного уравнения регрессии оказался равен 0,71511, то отсюда можно сделать вывод, что оно в 71,51% случаях в состоянии объяснить ежемесячные колебания курса доллара.

1.2. Значимость F равна 5,4E-60 или =0, а, следовательно, уравнение регрессии статистически значимо как при 95% уровне надежности, так и при 99% уровне надежности.

2.1. P-Значение для коэффициента свободного члена уравнения равно 0,023323, а следовательно этот коэффициент статистически значим лишь при 95% уровне надежности, но не значим при 99% уровне надежности, поскольку он больше 0,01. P-Значение для коэффициента регрессии равно 0, а, следовательно, этот коэффициент статистически значим как при 95% уровне надежности, так и при 99% уровне надежности .

2.2. Коэффициент свободного члена (константа) уравнения при переходе от столбца Нижние 99,0% к столбцу Верхние 99,0% меняет знак с минуса на плюс, а потому статистически не значим при 99% уровне надежности. При 95% уровне надежности смены знаков не происходит, а потому свободный член уравнения при данном уровне надежности статистически значим. Коэффициент регрессии статистически значим как при 95%, так и при 99% уровне надежности, поскольку и в том и другом случае смены знака у данного коэффициента не происходит. Следовательно, на основании таблицы 5 можно сделать вывод, что в целом уравнение регрессии и все его коэффициенты статистически значимы при 95% уровне надежности.

Как мы уже говорили ранее, уравнение регрессии – в отличие от обычных уравнений, оценивающих функциональную, то есть жестко детерминированную связь между переменными – дает прогноз зависимой переменной с учетом воздействия случайного фактора. Поэтому фактические значения результативного признака практически всегда отличаются от его расчетных (теоретических) значений. При этом случайная компонента (остаток) находится следующим образом.

Сначала находится прогнозируемый курс доллара, например, на апрель 2010 г. С учетом того, что порядковый номер апреля 2010 равен 215 (при июне 1992 г. =1), предсказываемый на этот месяц курс доллара может быть найден следующим образом:

Y расч.=0,1622*215++ 1,9958=36,8616

e = Y факт. – Y расч.= -7,573

Следовательно, прогноз, сделанный по данному уравнению регрессии, в апреле 2010 г. оказался выше фактического курса доллара на 7 руб. 57,3 коп. Вполне очевидно, что это слишком большая величина отклонения, чтобы данное уравнение регрессии можно было бы использовать для прогноза валютного курса. В свою очередь, чем ближе теоретические значения подходят к фактическим данным, тем лучше качество прогностической модели. Поскольку разница между фактическим и предсказываемым значением курса доллара (yфакт. – yрасч.) может быть как величиной положительной, так и отрицательной, то ошибка аппроксимации (подгонки модели к фактическим данным) следует определять как в абсолютных цифрах по модулю, так и в процентах модулю.