Знаете ли вы физику? - Страница 18

^{Рис. 78. Один из проектов «вечного движения»}

Возражение ошибочно. Нетрудно убедиться расчетом, что отвесные линии, проведенные на Земле в расстоянии 1 м одна от другой, составляют между собою угол, который в 23 000 раз больше, чем угол между лучами Солнца, направленными к тем же точкам. Что касается величины силы, побуждающей шар скатываться с края стола, длиною в 1 м, то она составляет примерно одну 10–миллионную долю веса шара. В условиях нашей задачи, т. е. при полном отсутствии сопротивлений, всякая сколь угодно малая сила должна привести тело в движение, как бы велика ни была его масса. В данном случае, впрочем, сила не так уж мала: она одного порядка величины с тою силою, которая порождает океанские приливы; последняя сила даже и в реальных условиях (т. е. при наличии сопротивлений) ощутительно проявляет свое действие.

46. На наклонной плоскости

Не следует думать, что в положении А брусок, оказывая на опорную плоскость большее удельное давление, испытывает и большее трение. Величина трения не зависит от размеров трущихся поверхностей. Поэтому если брусок скользил, преодолевая трение, в положении В, то он будет скользить и в положении А.

47. Два шара

1. При решении этой задачи нередко делают существенную ошибку: не принимают во внимание, что отвесно падающий шар движется только поступательно, между тем как шар, скатывающийся по плоскости, совершает, кроме поступательного движения, также и вращательное. Не свободны от этого недосмотра даже некоторые школьные учебники.

Какое влияние оказывает отмеченное обстоятельство на скорость скатывающегося тела, видно из следующего вычисления.

Потенциальная энергия шара, обусловленная его положением вверху наклонной плоскости, превращается при отвесном падении целиком в энергию поступательного движения, и из уравнения

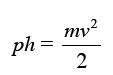
или (после замены веса р шара произведением его массы m на ускорение g тяжести) из равенства

легко получается скорость v такого шара в конце пути

где h – высота наклонной плоскости.

Иначе обстоит дело с шаром, скатывающимся по наклонной плоскости. В этом случае та же потенциальная энергия ph преобразуется в сумму двух кинетических энергий – в энергию поступательного движения со скоростью v₁ и вращательного – с угловою скоростью ω. Величина первой энергии равна

Вторая равна полупроизведению момента инерции K шара на квадрат его угловой скорости ω:

Имеем, следовательно, уравнение:

Из курса механики известно, что момент инерции K однородного шара массы т и радиуса r относительно оси, проходящей через центр, равен ²/₅ тr². Далее, легко сообразить, что угловая скорость ω этого шара, катящегося с поступательною скоростью v¹, равна

. Поэтому энергия вращательного движения

Заменив в нашем уравнении, кроме того, вес р шара равным ему выражением mg, получаем:

или, после упрощения,

gh = 0,7v₁².

Отсюда поступательная скорость

Сопоставляя эту скорость со скоростью в конце отвесного падения (

), видим, что они заметно различаются: скатившийся шар (любого радиуса и любой массы) в конце пути, да и в каждой его точке, движется вперед со скоростью на 16 % меньшею, чем шар, свободно упавший с той же высоты.

Сравнивая шар, скатывающийся по наклонной плоскости, с телом, скользящим по той же плоскости с равной высоты, легко установить, что скорость первого в каждой точке пути на 16 % меньше скорости второго.

Скользящий шар при отсутствии трения достигает конца наклонного пути раньше (на 16 %), нежели катящийся. То же верно и для тела, падающего отвесно: оно должно опередить скатывающийся шар на 16 %.

Кто знаком с историей физики, тому известно, что Галилей установил законы падения тел, производя опыты с шарами, которые он пускал по наклонному желобу (длина – 12 локтей, возвышение одного конца 1–2 локтя). После сказанного выше может возникнуть сомнение в правильности пути, избранного Галилеем. Сомнение, однако, отпадает, если вспомним, что скатывающийся шар в своем поступательном перемещении движется равноускоренно, так как в каждой точке наклонного желоба скорость его составляет одну и ту же долю (0,84) скорости отвесно падающего шара на том же уровне. Форма зависимости между пройденным путем и временем остается та же, что и для тела, свободно падающего. Поэтому Галилей и мог правильно установить законы падения тел в результате своих опытов с наклонным желобом.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.