Знаете ли вы физику? - Страница 16

Рис. 71. Нельзя натянуть веревку так, чтобы она между блоками не провисала
Никаким усилием, как бы велико оно ни было, нельзя натянуть веревки строго прямолинейно (кроме случая, когда она направлена отвесно). Провисание неизбежно; можно уменьшить его величину до желаемой степени, но нельзя свести его к нулю. Итак, всякая неотвесно натянутая веревка, всякий передаточный ремень должны провисать.
По той же причине невозможно, между прочим, натянуть и гамак так, чтобы веревки его были горизонтальны. Туго натянутая проволочная сетка кровати прогибается под грузом лежащего на ней человека. Гамак же, натяжение веревок которого гораздо слабее, при лежании на нем человека превращается в свешивающийся мешок.

Рис. 72. Гамак невозможно натянуть строго горизонтально
34. Увязший автомобиль
Силы одного человека часто оказывается достаточно, чтобы извлечь тяжелую машину тем примитивным способом, который описан в задаче. Веревка, при любой ее натянутости, должна уступить действию даже умеренной силы, приложенной под прямым углом к ее направлению. Причина С та же, какая заставляет провисать всякую натянутую веревку.
Возникающие при этом силы показаны на рис. 73. Сила CF тяги человека разлагается на две С CQ и СР, направленные вдоль веревки. Сила CQ тянет пень и, если он достаточно крепок, парализуется его сопротивлением. Сила же СР увлекает автомобиль, и так как она значительно больше, чем CF, то может извлечь машину из выбоины. Выигрыш силы тем больше, чем больше угол АСВ, т. е. чем сильнее натянута веревка.
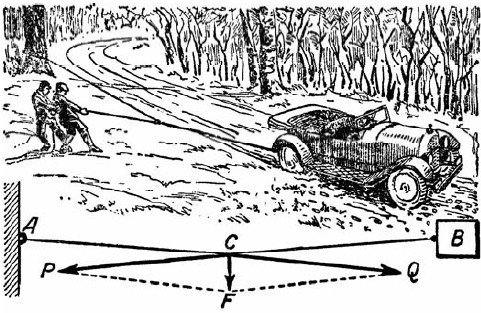
Рис. 73. Как вытащить автомобиль из выбоины
35. Трение и смазка
Смазка ослабляет трение средним числом раз в 10.
36. По воздуху и по льду
Можно думать, что так как сопротивление воздуха слабее, чем трение о лед, то тело, летящее через воздух, достигает дальше, чем скользящее по льду. Заключение это неправильно: оно не учитывает того, что сила тяжести пригибает вниз путь брошенного тела, которое вследствие этого и не может быть далеко закинуто. Сделаем расчет, причем ради упрощения выкладок будем считать сопротивление воздуха равным нулю. Оно, впрочем, и действительно крайне ничтожно для тех скоростей, какие можно сообщить телу рукой человека.
Для тел, брошенных в пустоте под углом к горизонту, наибольшая дальность достигается тогда, когда угол равен 45°. При этом, как выводится в курсах механики, дальность бросания определяется формулой:

=, где v – начальная скорость; g – ускорение тяжести. Если же тело скользит по поверхности другого тела (в данном случае лед по льду), то сообщенная ему кинетическая энергия
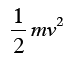
kmgL′.
Из уравнения

находим величину L′ пробега льдинки

Принимая коэффициент трения льда о лед равным 0,02, имеем

Между тем дальность бросания равна всего
Итак, заставив льдинку скользить по льду, мы можем закинуть ее раз в 25 дальше, чем бросив в воздух.
Если принять во внимание, что брошенная льдинка может продолжать двигаться и после падения, то дальность скольжения будет превышать дальность бросания уже не столь значительно; но и в таком случае преимущество на стороне скользящей, а не брошенной льдинки.
37. Падение тела
Падение тела «Тик – так» карманных часов длится не одну секунду, как часто думают, а только 0,4 с. Поэтому путь, проходимый падающим телом в этот промежуток времени, равен
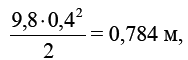
т. е. около 80 см.
38. Затяжной прыжок с парашютом
Противоречие объясняется тем, что падение с нераскрытым парашютом ошибочно принято было за свободное, не замедляемое сопротивлением воздуха. Между тем оно существенно отличается от падения в несопротивляющейся среде.
Попробуем установить, хотя бы приблизительно, подлинную картину падения при затяжном прыжке. Будем пользоваться для расчетов следующей найденной из опыта приближенной формулой для величины f сопротивления воздуха при рассматриваемых условиях:
f = 0,03 v2 кг,
где v – скорость падения в метрах в секунду. Сопротивление, как видим, пропорционально квадрату скорости; а так как парашютист падает с возрастающей скоростью, то наступает момент, когда сила сопротивления делается равной весу тела. С этого момента скорость падения расти больше не будет; падение из ускоренного становится равномерным.
Для парашютиста это наступает тогда, когда его вес (вместе с парашютом) сделается равным 0,03v2; принимая вес снаряженного парашютиста в 90 кг, имеем уравнение
0,03v2 = 90,
откуда v = 55 м/с.
Итак, парашютист падает ускоренно лишь до тех пор, пока не накопит скорости 55 м/с. Это наибольшая скорость, с какою он опускается, в дальнейшем скорость уже не возрастает. Определим – опять приближенно – сколько секунд употребил парашютист для достижения этой максимальной скорости. Примем во внимание, что в самом начале падения, пока скорость мала, сопротивление воздуха ничтожно, и тело падает как свободное, т. е. с ускорением 9,8 м/с. К концу же интервала ускоренного движения, когда устанавливается равномерное падение, ускорение равно нулю. Для нашего приближенного расчета можно допустить, что ускорение в среднем равнялось

Если принять таким образом, что секундная скорость нарастала на 4,9 м в секунду, то она достигает величины 55 м по истечении
55: 4,9 = 11 с.
Путь 5, проходимый телом в 11 секунд такого ускоренного движения, равен
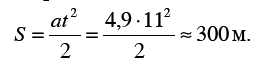
Теперь выясняется подлинная картина падения Евдокимова. Первые 11 с он падал с постепенно уменьшающимся ускорением, пока не накопил скорости 55 м/с, приблизительно на 300-м метре пути. Остальной путь затяжного прыжка он проходил равномерным движением со скоростью 55 м/с. Равномерное движение, согласно нашему приближенному расчету, длилось

а весь затяжной прыжок
11 + 138 = 149 с,
что мало отличается от действительной продолжительности (142 с).
Сделанный нами элементарный расчет надо рассматривать лишь как первое приближение к действительности, так как он основан на ряде упрощающих допущений.
Приведем для сравнения данные, полученные путем опыта: при весе снаряженного парашютиста 82 кг максимальная скорость устанавливается на 12-й секунде, когда парашют опускается на 425–460 м (Забелин, М. Прыжок с парашютом. М., 1933).