Звезды: их рождение, жизнь и смерть - Страница 98

Из наблюдаемого увеличения периодов пульсаров со временем можно получить

, а следовательно, и = .

Скорость уменьшения кинетической энергии вращения пульсара

(22.1)

Первая задача физики пульсаров — понять, почему вращающиеся нейтронные звезды тормозятся, тем самым непрерывно выделяя энергию. Простейшее объяснение этого явления сводится к тому, что нейтронные звезды сильно намагничены. Тогда вращающаяся нейтронная звезда, находящаяся в вакууме, будет излучать магнитно-дипольное излучение, частота которого равна частоте вращения, а мощность определяется формулой

(22.2)

где

 — угол между магнитной осью и осью вращения, H — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого = 200 с^-1, = 2,4 10^-9, теряет энергию = 3 10³⁸ эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая = L_m, найдем, что H 3 10¹² Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой

(22.3)

где I — момент инерции, а

_e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения.

Как видно из этой формулы, зависимость мощности гравитационного излучения от угловой скорости

значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?

Если бы торможение вращающихся нейтронных звезд было обусловлено их магнитно-дипольным излучением, то, как можно показать,

³. Между тем статистический анализ большого количества пульсаров с известными и дает эмпирическую зависимость ^3,4. У пульсара NP 0531, для которого и наблюдались особенно тщательно, эмпирическая зависимость имеет вид ^2,7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной.

Вращающийся намагниченный проводник создает в окружающем пространстве электрическое поле. Составляющая этого поля, перпендикулярная к поверхности проводника, будет стремиться «вырвать» из него электроны и ионы. В реальных условиях нейтронной звезды напряженность электрического поля достигает огромных значений. К тому же температура поверхности нейтронной звезды достаточно высока. По этим причинам пространство вокруг нейтронной звезды заполнится большим количеством заряженных частиц, которые, двигаясь по силовым линиям магнитного поля, будут вместе с нейтронной звездой с той же угловой скоростью вращаться вокруг ее оси. Такое «твердотельное» вращение должно иметь место вплоть до некоторого критического расстояния от оси вращения, т. е. внутри цилиндра. Радиус этого цилиндра R₁ = c/

определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света[ 54 ]. Однако если плотность плазмы вокруг нейтронной звезды достаточно велика, область ее твердотельного вращения будет меньше и определится условием равенства плотностей магнитной энергии и кинетической энергии плазмы.

Итак, вращающаяся намагниченная нейтронная звезда окружает себя довольно плотной магнитосферой, в электродинамическом смысле являющейся ее продолжением. Как показывают расчеты, электрические заряды в магнитосфере нейтронной звезды должны быть разделены, т. е. там должны быть значительные объемные заряды. Плотность зарядов определяется формулой

(22.4)

Например, на поверхности пульсара NP 0531, где H

3 10¹² Э, a = 200 с^-1, n_-- n₊ 10¹³ см^-3, т. е. довольно значительная. Конечно, полная плотность плазмы около поверхности этого пульсара должна быть гораздо больше.

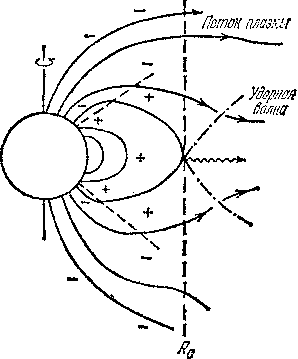Рис. 22.3: Rc

Заряженные частицы, предварительно ускорившись электрическим полем до релятивистских энергий, будут «вытекать» из магнитосферы на бесконечность по «открытым» силовым линиям, причем заряды разных знаков будут вытекать по разным линиям. На рис. 22.3 приведена схема магнитосферы пульсара для простейшего случая, когда магнитная ось совпадает с осью вращения. В случае, когда оси не совпадают, качественно структура магнитосферы остается такой же.