Юный техник, 2008 № 11 - Страница 14
Кроме того, ученикам всех отделений будет предложено участвовать в физико-математической олимпиаде «ФИЗТЕХ — 2009», которая будет проводиться на базе МФТИ и в ряде городов России в конце марта и в середине мая, в других очных и заочных олимпиадах МФТИ и его факультетов, а также в конкурсах, турнирах и конференциях. Для учащихся 9 — 11 классов на базе МФТИ работает субботний лекторий по физике и математике по программе ФЗФТШ. Лекции читают преподаватели института, как правило, авторы заданий. Подробнее об этих мероприятиях можно прочитать на сайте ФЗФТШ http://www.school.mipt.ru.
По окончании учебного года учащиеся, успешно выполнившие программу ФЗФТШ, переводятся в следующий класс, а выпускники (11 кл.) получают свидетельство об окончании школы с итоговыми оценками по физике и математике, которое учитывается на собеседовании при поступлении в МФТИ.
Ученикам, зачисленным в ФЗФТШ в рамках утвержденного плана приема, будет предложено оплатить безвозмездный целевой взнос для обеспечения учебного процесса в соответствии с уставными целями школы.
Для учащихся Украины работает Киевский филиал ФЗФТШ при МФТИ (обучение платное). Желающим в него поступить следует высылать работы по адресу: 03680, Украина, г. Киев, б-р Вернадского, д. 36, ГСП, Киевский филиал ФЗФТШ при МФТИ. Тел: 8-(10-38-044) 424-30-25, 8 (10-38-044) 422-95-64.
Для учащихся из зарубежных стран возможно только платное обучение на заочном и очно-заочном отделениях. Условия обучения для прошедших конкурсный отбор будут сообщены дополнительно.
Номера задач, обязательных для выполнения (заочное и очно-заочное отделения), приводятся в таблице:
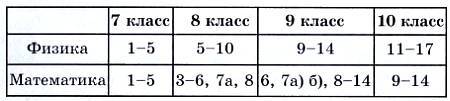
Номера классов указаны на текущий 2008–2009 учебный год.
МАТЕМАТИКА
После порядкового номера задачи в скобках указано количество очков за задачу
1(2). Мотоциклист ехал из пункта А в пункт В со скоростью 40 км/ч, а возвращался назад по той же дороге со скоростью 60 км/ч. Найдите среднюю скорость движения мотоциклиста за всю поездку.
2(3). Введите на клетчатой бумаге систему координат, отметьте точки А(-2; 4), В(-1; -1), С(-4; 10), D(-2; 5), Е(4; 7), F(10; 6), соедините их последовательно отрезками (АВ, ВС, CD, DE, EF, FA) и найдите площадь фигуры, которую они ограничивают. Площадь одной клетки считайте равной 1 см2.
3(4). В погребе замка лежало несколько пачек печенья. Ночью пришли крысы и съели 33 пачки, причем все ели поровну. У некоторых из них от обжорства заболели животы, поэтому на следующую ночь в погреб пришли не все крысы, а только 13 из них. Они доели оставшееся печенье, но каждая крыса смогла съесть втрое меньше печенья, чем накануне.
Сколько пачек печенья было на складе первоначально?
4(3). Незнайка и Пончик одновременно начали сбор земляники: Незнайка собирал ягоды в трех литровый бидон, а Пончик — в четырехлитровый, причем Незнайка собирал ягоды в 1,8 раза медленнее. В какой-то момент они поменялись бидонами и закончили сбор ягод одновременно (набрав полные бидоны).
Сколько литров земляники собрал Пончик за все время? А сколько он собрал ягод до обмена бидонами?
5(4). В семье четыре человека. Если Алисе удвоят стипендию, то общий доход всей семьи возрастет на 2,5 %, если вместо этого маме повысят зарплату в полтора раза — возрастет на 18,75 %, если же зарплату на 45 % повысят папе — возрастет на 18,45 %.
На сколько процентов возрастет доход всей семьи, если дедушке повысят пенсию на 20 %?
6(4). Для некоторых натуральных чисел n и k выполняется соотношение

(в числителе дроби записано произведение всех натуральных чисел от 1 до и, а в знаменателе — от 1 до k).
Найдите пик. Ответ обоснуйте.
7. Равнобедренный треугольник ABC с основанием АС поворачивают вокруг точки А на угол 30°, при этом точка В переходит в точку В1, точка С — в точку С1, а отрезок В1С1 проходит через точку С (рис. 1).
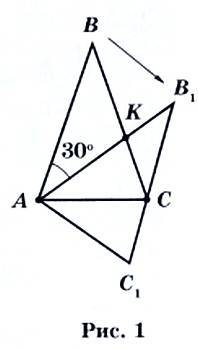
а)(4). Найдите расстояние от точки К до стороны АС (где К — это точка пересечения отрезков АВ1 и ВС), если известно, что АВ = 6.
б)(2). Найдите длину отрезка ВС1.
в)(2). Найдите площадь четырехугольника АВВ1С1.
8(4). Города А и В расположены на берегу реки, причем город В лежит ниже по течению. В 7 часов утра из А в В отправился плот, плывущий относительно берегов со скоростью течения реки. В 9 часов утра из В в А отправилась лодка, которая встретилась с плотом в 11 часов утра. Доплыв до города А, лодка мгновенно повернула обратно и приплыла в город Б одновременно с плотом.
В какое время они прибыли в город В?
9(3). Решите неравенство:
10(4). У одного человека был прямоугольный сад со сторонами 55 м и 40 м, и ему захотелось проложить в нем дорожку шириной 1 м, как показано на рисунке 2.

Чему равна площадь дорожки?
11(4). Фигура М на координатной плоскости состоит из точек, координаты которых удовлетворяют условиям:

Определите, при каком значении параметра k площадь фигуры М равна 20.
12(3). Найдите
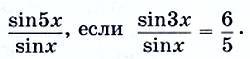
13(4). Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию:
14(5). При каких значениях параметра а уравнение х4 + (а — 3)х2 + (а + 10)2 = 0 имеет четыре корня, расположенные в порядке возрастания, причем эти четыре корня составляют арифметическую прогрессию?
ФИЗИКА
1. Стеклянная банка вмещает 3 л воды. Вес банки, целиком заполненной водой, составляет 40 Н. Определите объем стекла, из которого изготовлена банка. Плотность стекла ρс = 2500 кг/м3, плотность воды ρв = 1000 кг/м3, g= 10 Н/кг.
2. История сохранила некоторые подробности одного из последних путешествий таракана Митрофана по полу кухни. На графике (рис. 1) показано, как изменялось со временем расстояние от таракана до точки старта.
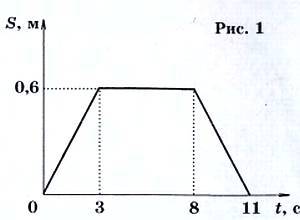
Известно, что все время таракан двигался с постоянной по величине скоростью, не проходя при этом одну точку дважды. Первые три и последние три секунды своего путешествия он двигался по прямой линии. Используя данные графика, определите модуль скорости таракана и пройденный им путь. Нарисуйте траекторию движения таракана в масштабе 1:10.