Восхождение на гору Невероятности - Страница 12
Пауки-крестовики, как правило, натягивают сеть с прицелом на первичный захват насекомого и уповают на то, что успеют добежать по паутине до жертвы и взять ее в плен раньше, чем она улетит. Другие пауки выбирают иной путь и плетут изначально рыхлую паутину (рис. 2.8). Пауки рода Pasilobus делают треугольник с одиночной нитью, рассекающей его надвое. Липкие нити – их всего несколько – не натянуты. Хитрость заключается в том – и это еще одно интересное открытие, которое сделали Майкл и Барбара Робинсон в Новой Гвинее, – что эти нити легко оборвать на одном из концов. Насекомое – скажем, муха, – влетев в паутину и прилипнув к ней, тут же обрывает нить у специально устроенного неустойчивого к обрыву узла, но все равно прилипает к другому концу нити. Дальше она крутится, словно игрушечный самолетик на веревочке. Теперь для паука вытянуть нить и прикончить жертву – дело техники. Такая схема имеет, в частности, все то же преимущество – поскольку конструкция болтается и нет точки опоры, насекомое не в состоянии бороться. А может быть, схема с рвущимися нитями хороша прежде всего тем, что позволяет решить уже известную нам задачу – погасить удар насекомого о сетку, когда оно влетает в нее на высокой скорости, так чтобы сетка не отбросила его, словно батут. Возможно, треугольная ловушка пауков Pasilobus – это сокращенная версия полной круговой паутины. Во всяком случае, пауки другого рода, Poecilohachys, плетут круговую паутину с тем же принципом действия. Их сети, в отличие от типичной круговой паутины, расположены не вертикально, а горизонтально.
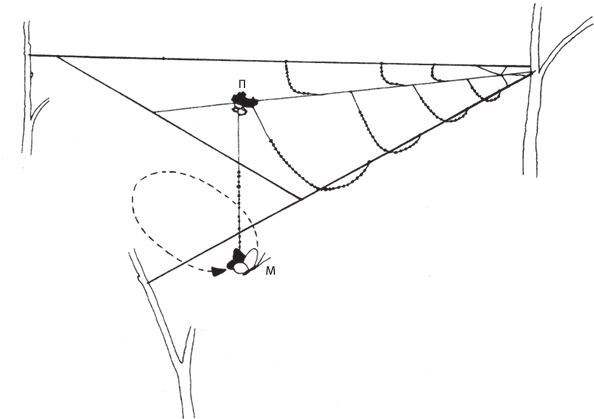
Рис. 2.8. Треугольная паутина паука Pasilobus с нитью, легко обрывающейся с одного конца.
Если рассматривать треугольник пауков Pasilobus как уменьшенный вариант этой полноценной круговой ловчей сети, то можно и дальше экстраполировать ряд вплоть до предельного случая – единичной нити с шариком на конце, которую используют пауки-арканщики (боладоры, род Mastophora, рис. 2.9). Болас, или бола, изобретение южноамериканских индейцев, напоминает пращу; нынешние скотоводы испано-индейского происхождения и сейчас его используют – например, чтобы ловить в прерии не умеющих летать нанду. Болас представляет собой веревку с грузом на конце, круглым камнем или каменным шаром. Груз кидают так, чтобы веревка обмотала ноги птицы и она упала. Чарльз Дарвин в молодости упражнялся с боласом, сидя верхом на лошади, и ухитрился ее же и изловить, чем здорово развеселил ковбоев… хотя лошадь вряд ли разделила их радость. На эту паучью удочку неизменно клюют самцы мотыльков-совок, или ночниц, и на то есть причина. Ночницы-самки приманивают партнеров издалека, испуская своеобразный аромат. Пауки выделяют вещество с похожим запахом, который увлекает мотыльков на верную гибель. Паучий “болас” – это увесистый шарик, закрепленный на конце шелковой нити, другой конец которой паук держит одной ногой. Он раскачивает болас, пока не обмотает мотылька, а затем подтягивает добычу к себе. Это гораздо более высокотехнологичное орудие, нежели примитивная ковбойская сумка с камнями. На самом деле это плотно скрученный шелковый канат, помещенный в каплю воды, наподобие клейких капель в круговой паутине. Когда паук забрасывает свой болас, канат разворачивается, словно леска спиннинга. Если он коснется мотылька, тот прилипнет, и шарик будет описывать круги. Далее события развиваются так же, как в сценарии с провисающими нитями. Туго спеленутый мотылек получает инъекцию яда. Пауки с боласами обитают в Южной Америке – кто знает, может индейцы, увидев, как охотятся пауки, взяли их идею на вооружение.
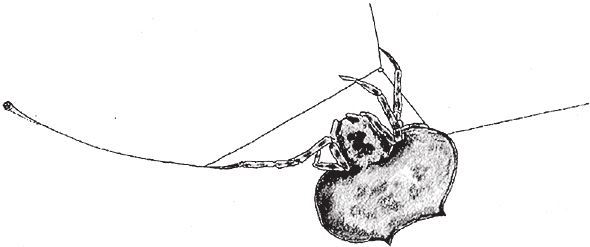
Рис. 2.9. Паук-арканщик (боладор).
Мы рассмотрели различные варианты полных и усеченных круговых паутин. Пора вернуться к собственно круговой паутине. В конце предыдущей главы мы задались вопросом о том, как с помощью программы биоморфов – компьютерной модели искусственного отбора – создать модель естественного отбора, где в роли селекционера выступал бы не человек, а равнодушная природа. Выяснилось, что биоморфы имеют существенный недостаток – у них нет ничего общего с реальным физическим миром, в котором надо выжить и либо победить, либо проиграть. Мы можем условиться, что какие‐то биоморфы будут хищниками, охотящимися на другие биоморфы – жертвы. Но непонятно, как естественным путем, без дополнительных условий догадаться, какие свойства биоморфов помогают или мешают им охотиться и уходить от преследования. У одного из биоморфов с рис. 1.16 (стр. 48) можно при желании различить страшные клыки, с которых капает хищническая слюна. Но его разверстая пасть неподвижна и не функционирует в живой природе, где клыки могли бы прокусить панцирь или шкуру, поэтому, как ни фантазируй, наяву этот кошмар не увидишь. Клыки и шкура – всего лишь комбинация пикселей на плоском светящемся экране. Острота зубов, сила, хрупкость и ядовитость – на экране монитора все эти параметры без придуманных описаний, которые программист произвольно облек бы в цифры, не имеют смысла. Можно протестировать ходилку-стрелялку типа “цифры против цифр”, но рисованное воплощение цифровых значений будет носить чисто косметический, не нужный для действия характер. Понятно, что придуманные описания и произвольные цифры в реальности ничего не означают. Вот на этом самом месте в конце предыдущей главы мы, вздохнув с облегчением, вернулись к теме паутины. Паутина – это природный объект, который можно воспроизвести без произвольных допущений.
В живой природе работающая круговая паутина плоская. Сквозь крупноячеистую сеть муха пролетит беспрепятственно. Если ячейки слишком мелкие, пауки-конкуренты добьются примерно тех же результатов при меньших затратах на шелк, а следовательно, оставят после себя больше потомства и передадут ему свои рационализаторские варианты генов. Естественный отбор приводит к разумному компромиссу. Нарисованная в компьютере паутина взаимодействует с такими же нарисованными мухами, причем ее свойства таковы, что взаимодействия отнюдь не произвольны. Размер ячеек – величина, вовсе не бессмысленная по сравнению с размерами компьютерной “мухи”. Столь же значимый параметр – суммарная длина линий (“затраты на шелк”). Сделав небольшую скидку на искусственность модели, можно рассчитать эффективность ловчей сети как соотношение этих величин. Можно даже учесть в компьютерной модели чуть более сложную физику – впервые это сделали Фриц Фольрат, у которого я и почерпнул многое из того, что здесь написал, и его коллеги, физики Лоррен Лин и Дональд Эдмондс. Гораздо проще описать “упругость” и “остаточную деформацию” компьютерной “паутины”, чем, скажем, “проворство” “убегающей” от цифрового “хищника” “жертвы” или ее “бдительность” при “определении его местонахождения”. Однако в этой главе нас больше интересует имитация процесса создания паутины.
Программист может записать правила для компьютерной модели паука, используя результаты полевых наблюдений – знания о повадках живых пауков и о критических моментах, которые определяют их линию поведения. Профессор Фольрат и его интернациональная исследовательская группа – бесспорные лидеры в этой области, и у них была прекрасная возможность подытожить свой опыт в компьютерной программе. Компьютерная программа действительно дает шанс систематизировать накопленные сведения о любом наборе правил. Собрать в компьютере имеющийся пул информации о зафиксированных наблюдателями движениях паука, который плетет паутину, вызывался Сэм Чокке, один из членов команды. Он назвал свою программу MoveWatch. Питер Фукс и Тимо Кринк, опираясь на работы Ника Готта и Алуна ап Ришарта, сосредоточились на обратной задаче – создании виртуальных “пауков”, которые ловят виртуальных “мух”. Эта программа получила название NetSpinner.