Вначале была аксиома. Гильберт. Основания математики - Страница 7
— аксиомы порядка, которые позволяют утверждать, что, например, «эта точка лежит между этими двумя» (как отметил Паш, данный тип аксиом полностью отсутствовал среди евклидовых постулатов);
— аксиомы конгруэнтности, определяющие соразмерность отрезков;
— аксиома параллельности имеет знаменитую формулировку о параллельных прямых;
— аксиомы непрерывности, их две: так называемая аксиома Архимеда, которая гласит, что если последовательно повторять любой из двух заданных произвольных отрезках, мы можем построить отрезок большего размера, чем первый, за конечное число шагов; и аксиома полноты линии, или непрерывности прямой, она гласит, что точки одной прямой образуют систему, неподверженную какому- либо расширению при условии сохранения линейного порядка и отсутствии противоречия аксиоме конгруэнтности и аксиоме Архимеда.
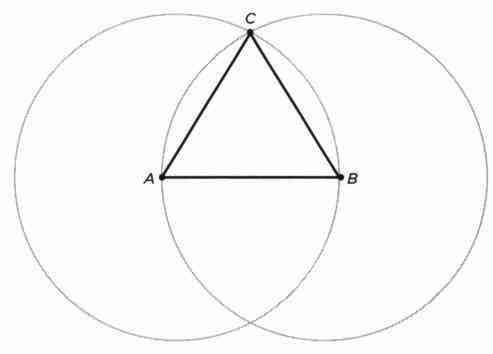
Без аксиомы непрерывности нельзя утверждать, что две окружности пересекутся в точке С и,следовательно, что можно построить равносторонний треугольник со стороной АВ (как это заявлено в Пропозиции I Книги I «Начал» Евклида).
Последней аксиомы в «Началах» не было, хотя необходимость в ней возникает даже при доказательстве Пропозиции I Книги I. То, что Гильберт извлек ее на свет, составляет один из важнейших его вкладов. Без нее Q2 (то есть плоскость, в которой у точек есть только рациональные координаты) было бы моделью евклидовой геометрии, поскольку она бы удовлетворяла всем предыдущим аксиомам. Однако, как подчеркнул Рихард Дедекинд (1831-1916), в этой дырявой плоскости две окружности, каждая из которых проходит через центр другой, необязательно должны пересекаться (что предполагалось в Пропозиции I), потому что это возможно в точке с иррациональными координатами (в дырке). Аксиома полноты линии, или непрерывности прямой, позволяет определить любую прямую с действительными числами R и, следовательно, плоскость R2 (то есть полную плоскость со всеми точками с рациональными и иррациональными координатами), где две окружности гарантированно пересекутся (см. рисунок). Это мост между синтетической геометрией, основанной на диаграммах и чертежах, и аналитической, выстраиваемой на вычислениях.
АКСИОМЫ, ДОКАЗАТЕЛЬСТВА, ТЕОРЕМЫ И ТЕОРИИ
С аксиоматической точки зрения аксиома — это высказывание, по той или иной причине (обычно из-за ее плодотворности) помещенное в основание математической теории, чтобы из него в дальнейшем можно было вывести теоремы. Но чтобы вывести теоремы, необходим свод правил выведения. Математики обычно оперируют двумя классическими правилами. Первое, modus ponens, заключается в том, чтобы из импликации «Если Р, то Q» и из истинности Р вывести, что истинно также Q. Второе, modus tollens, состоит в том, чтобы из импликации «Если Р, то Q» и из того, что Q ложно, вывести, что Ртакже ложно. Таким образом, формально доказательство — это цепочка рассуждений, которая позволяет получить новые результаты с применением аксиом и правил выведения. Конечным результатом доказательства называется теорема. Если на основе множества аксиом S мы смогли вывести теорему T, обычно это записывается как S ├ T («T доказуемо на основе S»), где знак ├ обозначает синтаксическое отношение выведения или доказательства. Теорией называют множество всех теорем, которые могут быть доказаны. Модель теории — математическая структура, в которой аксиомы истинны, они выполняются. Если М — это модель множества аксиом S, это записывается как М ╞ S («М выполняет S», то есть «аксиомы S истинны в М»). Знак ╞ обозначает семантическое отношение истинности или выполнения. Один из главных вопросов, которые поставил Гильберт, состоит в том, какое математическое отношение существует между отношением доказательства и отношением истинности (между ├ и ╞): истинно ли все доказуемое? Доказуемо ли все истинное?
Помимо формулировки аксиом, Гильберт стал первым, кто с чисто математического уровня в основе геометрии поднялся на метаматематический, или метагеометрический, уровень, где рассматриваются свойства любой аксиоматической системы, в частности той, которую он определил для геометрии. Какими свойствами должна обладать аксиома? Гильберт выделил три характеристики: независимость, непротиворечивость и полнота.
Аксиоматическая система является независимой, если ни одна аксиома не может быть выведена из другой, то есть если система максимально экономична, не избыточна. И пусть не все сформулированные им аксиомы оказались независимыми (как выяснилось позже), Гильберт доказал независимость между различными группами аксиом. Он утверждал, что аксиома параллельных прямых независима от прочих аксиом, то есть она не может быть выведена на их основе, чем закрыл вопрос, остававшийся открытым несколько столетий. Это стало возможным с применением метода, ставшего вскоре классическим: построить модели геометрий, которые выполняют все желаемые аксиомы, кроме той, независимость которой проверяется, и тогда последняя не может быть следствием из других (поскольку если бы это было так, мы получили бы противоречие — аксиому и ее отрицание). Для доказательства независимости аксиомы параллельных прямых Гильберт создал модель неевклидовой геометрии. А для доказательства независимости аксиомы Архимеда он построил модель неархимедовой геометрии, в которой существуют бесконечно малые величины. Так Гильберт, по примеру Джузеппе Веронезе (1845-1917), распахнул двери для исследования геометрии нового типа.

Давид Гильберт, 1886 год.

Скульптурная группа, воздвигнутая в память о Гауссе и Вебере в Гёттингене. Гильберт опубликовал свои«Основания геометрии» (1899) по случаю ее торжественного открытия.

Кёнигсбергский университет, около 1890 года. Гильберт поступил сюда десятью годами ранее.
Вторым требованием, которое Гильберт предъявлял к своей аксиоматической системе, была непротиворечивость. Система аксиом является непротиворечивой, если не порождает разногласий, если нельзя вывести никакого противоречия на ее основе. Такую систему аксиом называют когерентной, или совместимой. Модели Бельтрами, Клейна, Пуанкаре и Римана доказали относительную непротиворечивость неевклидовых геометрий в отношении к евклидовой, поскольку эти неевклидовы модели содержались внутри собственно евклидова пространства. Но была ли непротиворечивой евклидова геометрия? Гильберт доказал непротиворечивость евклидовой геометрии относительно арифметики, впервые предложив чисто числовую модель. Он вывел числовое множество, в котором выполняются все геометрические аксиомы, в котором точки — это некоторые пары алгебраических чисел, а прямые — некоторые тройки этих чисел, в котором принадлежность какой-то точки прямой означает, что соблюдается некое числовое уравнение, и так далее. Таким образом, любая противоречивость его аксиоматической системы геометрии привела бы к противоречивости арифметики. Любое противоречие в выводах, cделанных на основе геометрических аксиом, было бы признано арифметическим (например, 0=1).
ВЛИЯНИЕ ГЕРЦА
Не исключено, что Гильберт не был близко знаком с аксиоматическими работами итальянской школы Пеано, зато он знал о достижениях немецкой школы — как в области геометрии (Паш), так и в области механики. Генрих Рудольф Герц (1857-1894) скончался в возрасте 37 лет, но за свою короткую жизнь он успел удивить современников как физик-экспериментатор (он открыл электромагнитные волны и фотоэлектрический эффект) и физик-теоретик. В 1894 году он опубликовал работу «Принципы механики, изложенные в новой связи», в которой аксиоматически изложил знания в этой области. К собственной аксиоматической системе у него имелось два требования: допустимость и корректность. Допустимость совпадает с непротиворечивостью, с отсутствием противоречий. А корректность — с полнотой, с возможностью доказать в рамках этой теории все, что является истинным в мире. Эти два понятия перекликаются с введенными Давидом Гильбертом.