Веселые задачи. Две сотни головоломок - Страница 3

И в самом деле: садовник с изумлением убедился, что оставшиеся на корню 10 деревьев образуют 5 рядов по 4 дерева в каждом. Приказание его было исполнено буквально, – и все-таки вместо 29 деревьев работник вырубил 39.

Как же ухитрился он это сделать?

Все 13 мышей, окружающие эту кошку, обречены попасть ей на обед. Но кошка желает съесть их в определенном порядке, – а именно, каждый раз она отсчитывает 13-ю мышь по кругу в том направлении, в каком эти мыши глядят, – и съедает ее. С какой мыши она должна начать, чтобы белая оказалась съеденной последнею?

Рис. 9.

Из 18 спичек нетрудно сложить два четырехугольника так, чтобы один был вдвое больше другого по площади (рис. 10).

Рис. 10.

Но сложите из тех же спичек два таких четырехугольника, чтобы один был в три раза больше другого по площади!

Ниже указан самый короткий способ обмена. Цифры показывают, с какого пня на какой надо прыгать (напр., «1–5» значит: белка прыгает с пня 1-го на 5-й). Всех прыжков понадобится 16, а именно:

1-5; 3–7, 7–1; 8–4, 4–3, 3–7; 6–2, 2–8, 8–4, 4–3; 5–6, 6–2, 2–8; 1–5, 5–6; 7–1.

Для удобства мы заменим чайную посуду цифрами. Тогда задача представится в таком виде:

Надо обменять места 2 и 5. Вот порядок, в каком следует двигать предметы на свободный квадрат:

2, 5, 4, 2, 1, 3, 2, 4, 5, 1, 4, 2, 3, 4, 1, 5, 2.

Задача решается в 17 ходов – более короткого решения нет.

В этой таблице показаны в последовательном порядке все переезды, необходимые для того, чтобы вывести заведующего гаражом из затруднения. Цифры обозначают номера автомобилей, а буквы – соответствующие помещения. Всех переездов понадобится 43. Вот они:

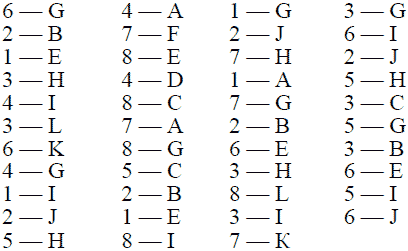
«6 – G» означает: автомобиль № 6 становится в отделение G, и т. п.

Три непересекающиеся пути показаны на этом чертеже:

Рис. 11.

Петру и Павлу приходится идти довольно извилистыми путями, – но зато братья избегают нежелательных встреч между собой.

Стрелки на рисунке показывают, какие мухи переменили место и с каких клеток oни пересели.

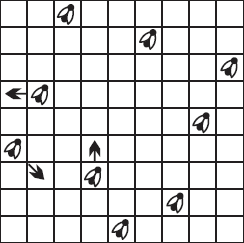
Рис. 12.

Забор можно построить двояко. Вот чертежи, показывающие направление ограды.

Забор, построенный по второму плану, короче и, следовательно, дешевле.

Рис. 13.

Вот единственное расположение, при котором два дома безопасны от нападения извне.

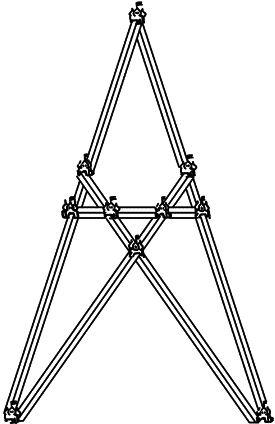
Рис. 14.

Вы видите, что 10 до мов расположены здесь, как требовалось в задаче: по 4 на каждой из пяти прямых стен.

Деревья, оставшиеся несрубленными, были расположены так (рис. 15):

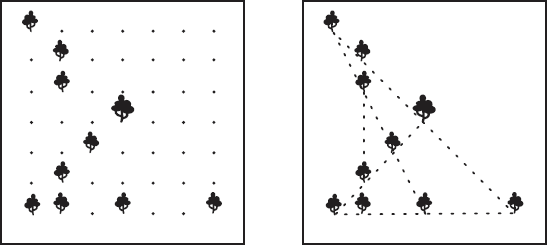
Рис. 15.

Как видите, они образуют 5 прямых рядов, и в каждом ряду 4 дерева.

Кошка должна съесть первой ту мышь, которая находится на нашем рисунке у копчика ее хвоста.

Попробуйте, начав с этой мыши счет по кругу, зачеркивать каждую 13-ю мышь, – вы убедитесь, что белая мышь будет зачеркнута последней.

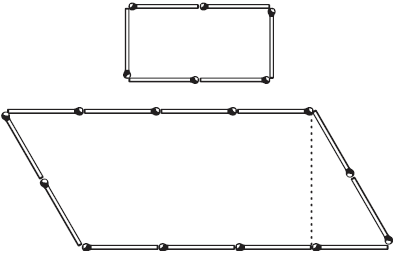
Рис. 16.

На чертеже показано, как надо сложить из 18 спичек два четырехугольника, чтобы один был втрое больше другого по площади. Вторым четырехугольником является параллелограмм с высотою, равною 1 ¹/₂ спичкам.

Площадь параллелограмма равна его основанию, умноженному на его высоту. В основании нашего параллелограмма лежат 4 спички, высота же равна 1 ¹/₂спичкам; следовательно, площадь равна 4 x 1¹/₂, т. е. 6таким квадратикам, каких в меньшем четырехугольнике 2. Итак, нижний четырехугольник имеет площадь втрое большую, нежели верхний.

В магазин доставили 6бочек керосину. На этом рисунке обозначено, сколько ведер было в каждой бочке. В первый же день нашлось два покупателя; один купил целиком две бочки, другой – три, причем первый купил вдвое менее керосина, чем второй. Не пришлось даже раскупоривать бочек.

Рис. 17.

И тогда на складе из 6 бочек осталась всего одна. Какая?

В бочке налита вода, по-видимому, до половины. Но вы хотите узнать точно, половина ли в ней налита, или больше половины, или же меньше половины. У вас нет ни палки, ни вообще инструмента для обмера бочки. Втулки бочка не имеет. Каким образом могли бы вы убедиться, налита ли вода ровно до половины?

Кстати, о полупустой бочке. Полупустая бочка – это ведь то же, что и полуполная. Но если половины равны, то должны быть равны и целые. Полупустая бочка равна полуполной, – значит, пустая бочка должна равняться полной. Выходит, что пустой равен полному!

Почему получился такой несообразный вывод?

Как вы думаете: существует ли на свете два человека с одинаковым числом волос?

Вы ответите, пожалуй, что два совершенно лысых человека имеют волос поровну, потому что и у того и у другого ноль волос.

Это, если хотите, правильно.

Но я спрашиваю не о безволосых людях, а о таких, у которых имеются на голове густые волосы. Найдется ли в мире два человека, у которых число волос на голове было бы в точности одинаково?

А может быть, двое таких людей отыщутся в Ленинграде или Москве?

Книга в переплете стоит 2 руб. 50 коп. Книга на 2 рубля дороже переплета. Сколько стоит переплет?

Иванов приобретает все нужные ему книги у знакомого ему книгопродавца со скидкою в 20 процентом. С 1-го января цены всех книг повышены на 20 процентов. Иванов решил, что он будет теперь платить за книги столько, сколько остальные покупатели платили до 1-го января. Прав ли он?

На лугу паслись лошади под надзором кучеров. Если бы вы пожелали сосчитать, сколько всех ног на лугу, то насчитали бы 82 ноги. А если бы пересчитали головы, то оказалось бы, что всех голов – лошадиных и человеческих – 26.