В поисках похищенной марки - Страница 33

— Значит, пиррова победа — победа мнимая! — воскликнул Нулик. — Тогда не хочу я, чтобы Магистр одержал такую победу.

— Очень вам признателен, ваше президентство, — сказал Сева. — Если можно, пожелайте ему также, чтобы он вернулся домой не на щите, а со щитом, как и полагается победителю. С вашего позволения, на щите приносили с поля брани только побеждённых.

После этого ехидного замечания заседание вошло в обычное русло, и мы занялись задачами. Первая же из них вызвала оживлённые споры.

В самом деле: есть у палки середина или нет? Для решения этого животрепещущего вопроса президент не пожалел даже собственного карандаша. Он сделал на нём ножом отметину посередине и разрезал пополам.

— Где середина? Нет её! — Затем Нулик снова соединил обе половинки карандаша. — Вот она, середина! — и снова разъединил. — Опять исчезла!

Так он играл довольно долго, ожидая, вероятно, исчерпывающего объяснения со стороны. Но объяснения всё не было. По правде говоря, я и сам не знал, каким образом объяснить ребятам этот забавный парадокс, чем-то похожий на софизмы Зено́на, которыми мы занимались ещё в прошлом году. Уж больно это не просто!

— Мне кажется, дело здесь в том, — решился я наконец, — что слово «середина» имеет смысл лишь тогда, когда речь идёт о целом отрезке, в данном случае о целом карандаше. Как только карандаш разрезан пополам, слово «середина» теряет свой смысл. Карандаш, как целое, исчез. Остались две его половинки, и у каждой из них своя середина. Кроме того, середина — это точка, а точка в математике — понятие условное. Нет у неё ни длины, ни ширины, ни толщины. Значит, условно и понятие «середина». Вообразить точку, называемую серединой, можно, но воткнуть в неё реально существующую иглу — пусть самую тонкую, самую острую — нельзя.

— Но ведь втыкаем же мы иглу циркуля в центр окружности? — возразил президент.

Конечно, втыкаем, но неглубоко, — пошутил я. — И так как всякому овощу своё время…

— …не станем углубляться в этот вопрос! Это вы хотели сказать? — спросил Нулик язвительно.

Я с сожалением развёл руками.

— Что делать!

— Понимаю! — вздохнул президент. — Переходим к следующей задаче.

— К той, что задал Магистру Главный Кубист и Шарист? — спросил Сева.

— К той самой, — кивнул Нулик. — И какой же он неблагодарный, этот Кубист и Шарист! Магистр решил его задачу, а он даже спасибо не сказал!

— С чего ты взял, что Магистр решил задачу?

— А разве нет? Ведь шар в самом деле можно вписать в куб, и в кубе после этого ещё останется немножко незаполненного места. Стало быть, объём и поверхность куба чуть больше, чем у шара.

— Положим, не чуть, — сказал Сева, — а примерно раза в два. Но дело ведь не в этом, а в том, сколько потребуется бумаги, чтобы обклеить шарики и кубики с увеличенными в восемь раз объёмами.

— Наверное, для этого надо узнать, во сколько раз увеличилась при этом поверхность, — сообразил Нулик.

— Наконец я слышу речь не мальчика, но мужа! — сказал Сева, не устояв перед соблазном лишний раз процитировать Пушкина. — И ты сейчас сам убедишься, что это совсем нетрудно.

— Кому как! — мрачно буркнул Нулик.

— Начнём с шара, — продолжал Сева, не обращая внимания на эту реплику. — Сперва займёмся его объёмом. Как и всякий объём, объём шара измеряется в кубических единицах и пропорционален кубу его радиуса. Значит, если объём увеличился в восемь раз, то радиус увеличился только в два раза.

— Как так?

— Очень просто — ведь корень кубический из восьми равен двум. Теперь выясним, что станет с поверхностью шара. Как известно, поверхность шара измеряется в квадратных единицах и пропорциональна квадрату радиуса. Выходит, если радиус увеличился вдвое, то поверхность шара увеличится в два в квадрате раза, то есть в четыре, а не в восемь раз, как полагает Магистр.

— Понятно! — хмуро согласился Нулик. — Но теперь нам предстоит ещё вычислить объём и поверхность куба.

— Ну это легче лёгкого. Ведь объём куба пропорционален кубу его ребра, а поверхность — квадрату этого ребра. Значит, увеличь объём куба в восемь раз, поверхность его, как и поверхность шара, само собой увеличится…

— … в четыре раза! — поспешно завершил президент.

Итак, с шарами и с кубами покончили. Теперь можно было перейти к самому главному: к шифру загадочного телефона. И тут, словно почувствовав, что дело касается его лично, проснулся и громко залаял Пончик.

— Учуял преступников! — многозначительно поднял палец президент. — Собаки — у них такая интуа́ция…

— Интуи́ция, Нулик, интуиция! — ангельским тоном поправил Сева и без всякого перехода спросил: — Кто из нас займётся вскрытием сейфа?

— Дело тёмное, — сказала Таня. — Поэтому предоставим его Олегу.

— Как опытный взломщик, могу сказать, что дело не такое уж тёмное, — усмехнулся Олег. — Была бы ты чуть внимательнее, так разгадала бы шифр сама.

— Я только одно знаю, — заявил Нулик, что в этом шифре десять цифр. Потому что дверца сейфа открылась после десяти поворотов диска.

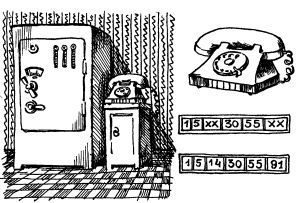
— Весь вопрос в том, что это за цифры! — сказал Олег. — Давайте внимательно всмотримся в запись Единички. Что там написано? Там написано вот что:

1 5 xx 30 55 xx.

Неизвестными в этом шифре остаются два двузначных числа — те, что были в третьем и последнем карманчиках. Как их найти?

— Надо поискать, нет ли между числами этого ряда какой-нибудь зависимости, — предложила Таня. — Вот, например, разность между вторым и первым числом, то есть между пятью и единицей, равна четырём…

— Разность между 55 и 30 равна 25, — продолжал Сева.

— И какой из этого вывод? — недоумевал Нулик.

— Да такой, что 4 и 25 — это квадраты целых чисел, — объяснил Олег.

— А ведь верно! — обрадовался Нулик. — 4 — квадрат двух, а 25 — квадрат пяти. Так, может быть, разности между другими соседними числами тоже квадраты?

— Добавь, квадраты последовательных целых чисел, — уточнила Таня. — Если это так, то здесь за квадратом двух должен следовать квадрат трех, то есть 9. Тогда в третьем карманчике должно стоять число 14. Потому что 14 минус 5 как раз и есть 9.

— Ну конечно! — ликовал Сева. — А разность между 30 и 14 равна 16, то есть квадрату следующего натурального числа — четырех.

— Выходит, — сосредоточенно соображал Нулик, — в последнем карманчике должно стоять число 55 плюс квадрат шести, то есть 55 плюс 36. А это 91.

— Вот спасибо! — сказал Олег, посылая Нулику воздушный поцелуй. — Теперь вместо крестиков впишем найденные числа, и шифр готов:

Вот в какой последовательности набирала Единичка цифры на диске.

— Леди и джентльмены, — торжественно провозгласил Сева, — сейф открыт!

— Сейф-то открыт, — вздохнул Нулик, — а Магистр с Единичкой в ловушке. Просто не знаю, как я доживу до следующего письма…

— Не горюй, старик! — ободрил его Сева. — Мы ещё чокнемся апельсиновым соком в честь благополучного возвращения наших путешественников!

Напрасно я усомнился в своём везении. Пусть, как царя Поликра́та, сжимает меня кольцо неудач, — смеётся всё-таки тот, кто смеётся последний!

Трое злоумышленников, то бишь Чёрный Лев, Шейк-Твист делла Румба и Альбертини-Джерамини, вывинтили единственную в комнате электрическую лампочку, заперли нас на ключ и ушли, прихватив с собой содержимое сейфа. И вот мы с Единичкой оказались одни, в темноте, отрезанные от всего мира.

В таком положении, как известно, не остаётся ничего другого, как заняться размышлениями. Между нами говоря, я до некоторой степени даже благодарен моим тюремщикам — ведь из-за них я получил возможность отвлечься от повседневной суеты и сосредоточиться на важных и безотлагательных проблемах. Во-первых, необходимо было составить подробный отчёт о моей поездке, во-вторых, придумать способ выбраться из заточения и, наконец, в-третьих, решить одну сложнейшую математическую задачу, над которой я бьюсь уже три года.