Тесты и их решения по финансовой математике - Страница 5

1-шаг (расчет

): 2^nd ICONV; 2^nd CLR WORK; (NOM=) 15 ENTER; ↑(C/Y=) 4 ENTER; ↑(EFF=) CPT: EFF = 15.865;

↓ (C/Y=) 12 ENTER; ↓ (NOM=) CPT: NOM=14.8163;

/12 =1.2347 %;

Продолжая, в силу (1.2) имеем

2-шаг (расчет

): :100 (переход от % к числовому значению); +1=; (функция деления); 14.8163 %=14.64 %.

Решение на компьютере.

1-шаг (

): ЭФФЕКТ(Номинальная ставка=15 %; Кол_пер=4)= 15.865 %;

2-шаг (

): ↓ НОМИНАЛ(Факт_ ставка=14.934 %; Кол_пер=4)= 14.8163 % ;

Далее, силу (1.2) имеем

3-шаг (расчет

): 14.8163 % / (1+14.8163 %/12)=14.64 %.

Первоначальный депозит в фонд: 40000.

Снятия денег из фонда в конце четвертого года: 50000.

Величина фонда в конце восьмого года: 15000.

Других депозитов или снятий денег в течение 8-летнего периода не было.

В каком интервале находится годовая ставка доходности в течение восьмилетнего периода?

A. Меньше 8%

B. 8 %, но меньше 10%

C. 10 %, но меньше 12%

D. 12 %, но меньше 14%

E. 14 % или больше

Решение.

Уравнение стоимости для данного депозита в конечной (8-й) точке имеет вид

Cледовательно, обозначая

и решая при этом полученное квадратное уравнение, находим

Решение на калкуляторе.

Выше данную диаграмму можно рассматривать как финансовый поток с платежами в конце года

Поэтому пользуясь функцией расчета «Внутренняя ставка доходности (IRR)»

получим

1-шаг (расчет i): 2nd RESET ENTER; CF;

40000 +/– ENTER: CF0= -40000;

↓; 1 ENTER: C01 = 0;

↓; 3 ENTER: F01 = 3;

↓; 50000 ENTER: C02 = 50000;

↓; 1 ENTER: F02 = 1;

↓; 15000 ENTER: C03 = 15000;

↓; 1 ENTER: F03 = 1;

IRR; CPT: IRR= 10.67 %.

Решение на компьютере.

1-шаг (расчет i): ВСД(-40000; 0; 0; 0; 50000; 0; 0; 0; 15000)= 10.67 %.

ТЕСТ 3

Постоянный, переменный, бессрочный аннуитеты

Рассмотрим следующие данные:

Дата выдачи ссуды: 01.01.1993.

Сумма ссуды: 6 200.

Дата первого платежа: 31.01.1993.

Частота платежей: ежемесячно.

Количество платежей: 60

Размер каждого из первых: 59 платежей: 100.

Процентная ставка: 9,00 % в год, начисляемых ежемесячно.

В каком интервале находится размер последнего платежа?

A. Меньше 1800

B. 1800, но меньше 2000

C. 2000, но меньше 2200

D. 2200, но меньше 2400

E. 2400 или больше

Решение:

Пусть

и 60-й платеж обозначим через X. Тогда добавляя и отнимая этому платежу платеж в размере 100 и собирая все эти платежи в 60-й точке, имеем

.

Отсюда

=

.

Решение на калкуляторе.

1-шаг (расчет X-100): 2nd RESET ENTER; 2nd P/Y 1 ENTER; 2nd QUIT;

60 N; 9/12=0.75 I/Y; -6200 PV; 100 PMT; CPT FV: FV= 2165;

2-шаг (расчет X): +100=2265.

Решение на компьютере.

1-шаг (расчет X-100): БС(Ставка=9 %/12=0.75 %; Кпер=60; Плт=100; Пс=-6200; Тип=0) = 2165;

2-шаг (расчет X): 2165+100=2265.

Рассмотрим следующие данные:

Дата начала выплат по бессрочному аннуитету: 1/1/91

Процентная ставка: 9 % в год, начисляемых ежегодно

В каком интервале находится стоимость бессрочного аннуитета на 01.01.1991?

A. Меньше 1 050

B. 1 050, но меньше 1 100

C. 1 100, но меньше 1 150

D. 1 150, но меньше 1 200

E. 1 200 или больше

Решение.

Из данной диаграммы нетрудно составить уравнение стоимости для текущей стоимости данного аннуитета

PV= 20

.

Отсюда, учитывая формулу (см. (3.31) из [1])

получим

PV=

.

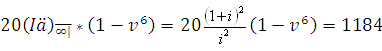
Рассмотрим следующие данные:

Дата выдачи ссуды: 1/1/95.

Сумма ссуды: 15 000.

Дата первого платежа: 30/06/95.

Частота платежей: каждые полгода.

Количество платежей: 60.

Сумма каждого платежа: увеличивается на 5 % каждые шесть месяцев.

Процентная ставка: 12 % в год, начисляемых каждые полгода.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.