Теория струн и скрытые измерения вселенной - Страница 36

Но существуют и еще более серьезные математические проблемы. Тогда как простейшие уравнения Монжа-Ампера содержат только две переменные, в более сложных случаях количество переменных значительно больше двух. Эти уравнения выходят за рамки гиперболических — их иногда называют ультрагиперболическими, и о их возможных решениях мы знаем еще меньше. Как заметил Калаби: «Мы понятия не имеем об этих других решениях, лежащих за пределами трех известных нам, поскольку мы совершенно не способны представить соответствующую им физическую картину».[48] Из-за неодинаковой сложности трех типов уравнений в геометрическом анализе на сегодняшний день используются в основном либо эллиптические, либо параболические уравнения. Конечно, мы заинтересованы во всех трех типах уравнений, и существует множество интереснейших задач, связанных с гиперболическими уравнениями, например уравнения поля Эйнштейна, но обратиться к их решению нам мешает отсутствие необходимых для этого инструментов.

Уравнения, используемые в гипотезе Калаби, были нелинейными эллиптическими. Несмотря на связь этих уравнений с гиперболическими уравнениями поля Эйнштейна, гипотеза Калаби основана на несколько иных геометрических структурах. В рассматриваемом нами случае мы предполагаем, что время в нашей задаче остановилось, почти как в известной сцене из «Спящей красавицы», где на протяжении сотни лет никто и ничто не может сдвинуться с места. Благодаря этому допущению в доказательстве гипотезы Калаби можно было использовать эллиптические уравнения, устранив зависимость от времени. Это стало причиной, по которой я надеялся на то, что инструменты геометрического анализа — и в том числе те, о которых уже было сказано выше, — смогут быть с успехом использованы для решения нашей задачи.

Впрочем, даже имея в своем распоряжении все необходимые инструменты, мне предстояло проделать немалую подготовительную работу. Частично это было обусловлено тем, что никто до меня не решал комплексные уравнения Монжа-Ампера для случая более чем одного измерения. Как альпинист, постоянно стремящийся к покорению новых высот, я стремился к покорению более высоких размерностей. Чтобы подготовить себя к схватке с многомерным уравнениям Монжа-Ампера, нелинейность которых сама собой подразумевалась, мы с моим другом Ш. Ченгом принялись за исследование различных многомерных случаев, начав с задач в вещественных числах с целью впоследствии перейти к более сложным комплексным уравнениям.

Для начала мы рассмотрели знаменитую задачу, выдвинутую на рубеже XX века Германом Минковским. Задача Минковского состояла в том, чтобы установить возможность или невозможность существования некоей структуры, удовлетворяющей определенному набору критериев. Рассмотрим простой многогранник. Его структуру можно охарактеризовать, подсчитав число граней и ребер и определив их размеры. Задача Минковского состояла в обратном: можно ли, зная форму, площадь, число и ориентацию граней, определить, существует ли в действительности многогранник, удовлетворяющий данным критериям, и если да, то будет ли он единственным?

Задача на самом деле была более общей, поскольку имела отношение не только к многогранникам, но и в принципе к любым выпуклым поверхностям. Вместо того чтобы говорить об ориентации граней, с равным успехом можно говорить о кривизне, указав для каждой точки поверхности направление перпендикулярных к ней — нормальных векторов, что соответствует ориентации поверхности в пространстве. После этого уже можно задаться вопросом, существует ли объект с указанной кривизной.

Удобно, что эта задача может быть представлена не только в геометрической форме. Она также может быть записана в виде дифференциального уравнения в частных производных. По словам Эрвина Лутвака из Политехнического института при Нью-Йоркском университете: «Если вы сможете решить геометрическую задачу, то автоматически получите дополнительный приз: решение сложнейшего дифференциального уравнения в частных производных. Такая взаимосвязь между геометрией и дифференциальными уравнениями в частных производных делает эту задачу столь важной».[49]

Мы с Ченгом нашли способ решения этой задачи, и наша статья, посвященная этому вопросу, вышла в 1976 году. Как выяснилось, другое решение было представлено несколькими годами раньше — в 1971 году российским математиком Алексеем Погореловым. Ни я, ни Ченг никогда не видели его статьи, поскольку она была опубликована на родном языке Погорелова. В конце концов, все свелось к решению сложнейшего дифференциального уравнения в частных производных из тех, которые никогда до этого не решались.

Несмотря на то что никому до нас не удавалось решить проблему данного типа, за исключением Погорелова, работа которого была нам неизвестна, процедура, позволяющая работать с нелинейными дифференциальными уравнениями в частных производных, на тот момент была уже хорошо разработана. Метод работы с подобными уравнениями, получивший название метода непрерывности, был основан на использовании последовательных приближений. И хотя этот общий подход никоим образом нельзя было назвать новым, особенность состояла в том, что каждая конкретная задача предусматривала разработку своей собственной стратегии, необходимой для ее решения. Основная идея заключалась в последовательной аппроксимации решения различными функциями так, чтобы каждое следующее приближение давало результаты лучше, чем предыдущее. Суть доказательства состояла в том, чтобы показать, что после достаточно большого числа итераций приближенная функция с большой точностью совпадет с решением искомого дифференциального уравнения. В случае удачи полученное путем аппроксимации приближение нужно рассматривать не как решение дифференциального уравнения, которое можно представить в виде определенной формулы, а как доказательство того факта, что решение существует. Для гипотезы Калаби и других задач того же типа существование решения дифференциального уравнения в частных производных эквивалентно доказательству существования определенной геометрии для заданных «топологических» условий. Это не означает, что вы ничего не знаете о решении, существование которого только что доказали. Схема, которая была использована для доказательства существования решения, зачастую может быть легко преобразована в численный метод для приближенного решения на компьютере. О численных методах речь пойдет в девятой главе.

Рис. 5.1. Математик Ш. Ю. Ченг (фотография Джорджа М. Бергмана)

Метод непрерывности был назван так потому, что он подразумевает непрерывное преобразование решения некоего известного уравнения вплоть до его полного совпадения с решением искомого. Процедуру преобразования, как правило, разбивают на две части, одна из которых работает только в непосредственной близости от известного решения.

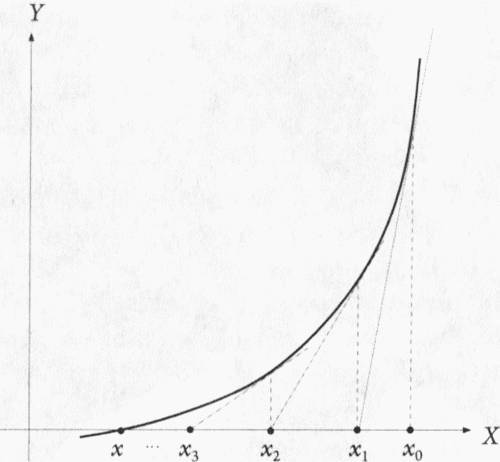
Рис. 5.2. Наглядная иллюстрация метода Ньютона. Для того чтобы найти точку пересечения определенной кривой или функции с осью X, сначала нужно наугад подобрать некую точку x₀ наиболее подходящую для этого. Затем необходимо провести касательную к кривой в точке x₀ и отметить точку, в которой эта касательная пересечет ось X (это будет точка x₁). В том случае, если наше изначальное предположение не было полностью ошибочным, продолжая этот процесс, мы будем получать точки все ближе и ближе к искомой

Одна из этих частей носит название метода Ньютона, так как она в определенной степени основана на методе, разработанном Исааком Ньютоном более трехсот лет назад. Для того чтобы продемонстрировать этот метод в действии, рассмотрим функцию y=x³-3x+1, которая описывает кривую, пересекающую ось X в трех различных точках, являющихся корнями этого полинома. Подход, предложенный Ньютоном, позволяет определить положение корней на оси X, что далеко не всегда можно сделать, просто взглянув на уравнение. Предположим, что напрямую решить уравнение нельзя, однако один из корней соответствующей функции можно найти вблизи точки x₁. Касательная, проведенная к кривой в этой точке, пересечет ось X в другой точке — x₂, находящейся ближе к искомому корню, чем точка x₁. Если мы проведем касательную в точке x₂, она пересечет ось X в точке x₃, которая будет еще ближе к искомому корню. Таким образом, многократное повторение данной процедуры должно довольно быстро привести нас к искомому корню, если только начальная точка x₁ была выбрана более-менее удачно.