Теория струн и скрытые измерения вселенной - Страница 29

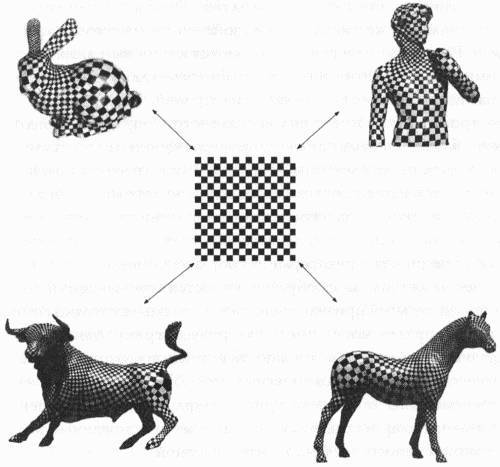
Рис. 4.2. Все эти двухмерные поверхности — бык, кролик, Давид и лошадь — являются примерами римановых поверхностей, имеющих огромную важность в математике и теории струн. Можно нанести на эти поверхности узор в виде шахматной доски, выбирая точки на шахматной доске, подставляя их координаты в некую функцию и получая в результате точку на поверхности, например кролика. Однако полученная в результате шахматная доска не будет идеальной, если только ее не отобразили на поверхность двухмерного тора, по причине присутствия на ней сингулярных точек, таких как северный и южный полюсы сферы, которые неизбежно возникают на поверхностях, эйлеровы характеристики которых (понятие эйлеровой характеристики будет подробно описано далее) не равны нулю. При этом, однако, процесс отображения является конформным, то есть углы — в том числе и прямые углы шахматной доски — при переходе от одной поверхности к другой всегда сохраняются. Несмотря на то что размеры объектов, таких как клетки шахматной доски, могут в результате оказаться искаженными, углы клеток все равно будут составлять ровно 90 градусов. Это свойство сохранения углов является одной из характерных особенностей римановых поверхностей

Пространства, которые представил себе Калаби, были не только комплексными, но также имели особое свойство, называемое кэлеровой метрикой. Римановы поверхности являются кэлеровым автоматически, поэтому данное понятие обретает смысл только для комплексных многообразий двух и более комплексных измерений. В кэлеровом многообразии пространство имеет вид евклидового в определенной точке и остается близким к нему при небольшом смещении, хотя и отклоняется от евклидовости определенным образом. Для того чтобы пояснить последнее утверждение, необходимо отметить, что это многообразие имеет вид не привычного плоского евклидового пространства, а так называемого «комплексного евклидового пространства», то есть оно имеет четную размерность и некоторые из координат, определяющие положение точек на данном многообразии, являются комплексными числами. Этот отличительный признак очень важен, поскольку только комплексные многообразия могут иметь кэлерову метрику. Данная метрика в свою очередь дает нам возможность помимо всего прочего измерять расстояния при помощи комплексных чисел. Условие Кэлера, названное в честь немецкого математика Эриха Кэлера, показывает степень близости заданного пространства к евклидовому на основании критериев, не связанных непосредственно с его кривизной.

Для того чтобы количественно оценить степень близости определенного многообразия к евклидовому пространству, необходимо знать его метрику. В плоском пространстве с взаимно перпендикулярными координатными осями для расчета расстояний можно использовать теорему Пифагора. В искривленных пространствах дело обстоит несколько сложнее, поскольку оси координат в этом случае могут уже не быть взаимно перпендикулярными, что приводит к необходимости использования модифицированной версии теоремы Пифагора. Для расчета расстояний в искривленных пространствах необходимо знать метрические коэффициенты — набор чисел, изменяющийся от точки к точке и зависящий от ориентации координатных осей. Выбор той или иной ориентации осей ведет к возникновению разных наборов метрических коэффициентов. При этом значение имеют не столько величины этих коэффициентов, которые во многом произвольны, сколько характер их изменения при переходе от одной точки многообразия к другой. Это дает возможность узнать положение различных точек по отношению друг к другу и таким образом свести воедино все, что касается геометрии данного многообразия. Как уже было сказано в предыдущих главах, для описания четырехмерного пространства необходимы десять метрических коэффициентов. На самом деле коэффициентов всего шестнадцать, поскольку метрический тензор в данном случае представляет собой матрицу 4×4. Однако метрический тензор всегда симметричен относительно диагонали, проходящей из левого верхнего угла матрицы в правый нижний. Таким образом, четыре числа лежат непосредственно на диагонали матрицы и еще два одинаковых набора из шести чисел каждый лежат по разные стороны от нее. За счет наличия симметрии вместо шестнадцати чисел можно рассматривать только десять: четыре на диагонали и шесть — по одну сторону от нее.

Это, впрочем, еще не объясняет механизм работы метрики. Рассмотрим весьма простой пример, имеющий место для одного комплексного или двух вещественных измерений, — метрику Пуанкаре единичного круга, центр которого находится в точке плоскости с координатами (0, 0). Этот круг представляет собой набор точек (x, y), удовлетворяющих неравенству x² + y² < 1. Формально такой круг называют «открытым», поскольку он не включает в себя свою границу — окружность, определяемую выражением x² + y² = 1. Поскольку рассматриваемый случай относится к двум измерениям, тензор метрики Пуанкаре представляет собой матрицу 2×2. В каждой из ячеек этой матрицы стоит коэффициент вида G_ij, где i — номер строки, j — номер столбца. Таким образом, матрица будет иметь вид:

G₁₁ G₁₂

G₂₁ G₂₂

За счет симметрии, о которой шла речь выше, G₁₂ будет равно G₂₁. Для метрики Пуанкаре эти два «недиагональных» элемента по определению равны нулю. Равенство двух других элементов — G₁₁ и G₂₂ не обязательно, но в случае метрики Пуанкаре оно имеет место: оба эти элемента по определению равны 4/(1-x²-y²)². Любой паре координат x и y, выбранной внутри единичного круга, метрический тензор ставит в соответствие определенный набор коэффициентов. Так, например, для x = 1/2 и y = 1/2 элементы G₁₁ и G₂₂ будут оба равны 16, оставшиеся же два коэффициента равны нулю для любой точки единичного круга.

Что же делать дальше с полученными числами? И как эти коэффициенты соотносятся с расстоянием? Нарисуем внутри единичного круга небольшую кривую, однако рассмотрим ее не как неподвижный объект, а как траекторию частицы, движущейся из точки А в точку В. Чему же равна длина этой траектории для данной метрики Пуанкаре?

Для того чтобы ответить на этот вопрос, рассмотрим кривую s и разделим ее на крошечные линейные участки — настолько крошечные, насколько это только можно представить, — и сложим их длины между собой. Длину каждого из линейных участков можно найти при помощи теоремы Пифагора. Для начала определим величины x, y и s параметрически, то есть представим их как функции времени: x = X(t), y = Y(t) и s = S(t). Производные этих функций — X'(t) и Y'(t) — можно рассматривать как катеты прямоугольного треугольника; их подстановка в теорему Пифагора √([X'(t)]²+[Y'(t)]²) дает значение производной S'(t). Интегрирование от А до В позволяет определить длину всей кривой. В свою очередь каждый линейный сегмент представляет собой касательную к кривой, называемую в данном случае касательным вектором. Однако поскольку кривая находится на круге Пуанкаре, то перед интегрированием полученный результат нужно умножить на значение метрики √([X'(t)]²+[Y'(t)]²)×√(4/(1-x²-y²)²), чтобы ввести поправку на кривизну.

Для дальнейшего упрощения полученной картины приравняем Y(t) к нулю и таким образом ограничимся осью x. Затем начнем движение с постоянной скоростью вдоль оси x из точки 0 в точку 1. Если время также будет изменяться от 0 до 1, то уравнение движения будет иметь вид X(t) = t, и при Y(t) = 0, что предполагалось изначально, производная X'(t) = 1, поскольку производная от X в данном случае берется по отношению ко времени, а значение X всегда равно значению времени. Если представить производную в виде отношения, то последнее уравнение станет очевидным: в этом примере производная по X — это отношение изменения переменной X к изменению переменной X, а любое отношение такого вида — с одинаковым числителем и знаменателем — всегда равно 1.