Теория струн и скрытые измерения вселенной - Страница 12

Рис. 2.3. На поверхности с положительной кривизной (такой, как сфера) сумма углов треугольника больше 180°, и линии, кажущиеся параллельными (такие, как меридианы) могут пересечься, например, на Северном и Южном полюсах. На плоской поверхности (поверхности с нулевой кривизной), которая является основой евклидовой геометрии, сумма углов треугольника равна 180°, и параллельные линии не пересекаются. На поверхности с отрицательной кривизной, например имеющей форму седла, сумма углов треугольника меньше 180°, а линии, кажущиеся параллельными, на самом деле расходятся

Эти принципы, являющиеся ключевыми для евклидовой геометрии, не выполняются в искривленных пространствах. Рассмотрим сферическое пространство, подобное поверхности глобуса. Если смотреть на глобус со стороны экватора, линии меридианов кажутся параллельными, поскольку все они перпендикулярны экватору. Но если вы проследуете по ним в одном из двух направлений, то увидите, что они в конце концов сходятся на Северном и Южном полюсах. Этого не произойдет в плоском евклидовом пространстве, таком как карта в проекции Меркатора, на которой две линии, перпендикулярные третьей, являются действительно параллельными и никогда не пересекаются.

В неевклидовом пространстве сумма углов треугольника может быть или больше, или меньше, чем 180°, в зависимости от того, как искривлено пространство. Если пространство, подобно сфере, имеет положительную кривизну, сумма углов треугольника всегда будет больше 180°. И напротив, если пространство имеет отрицательную кривизну, как внутренняя часть седла, сумма углов треугольника всегда будет меньше 180°. Узнать кривизну пространства можно, определив величину, на которую сумма углов треугольника больше или меньше 180°.

Гаусс также ввел понятие внутренней геометрии — идею, согласно которой объект или поверхность имеет свою собственную кривизну (так называемую гауссову кривизну), которая не зависит от того, как этот объект располагается в пространстве. Рассмотрим для примера лист бумаги. Можно ожидать, что его кривизна равна нулю, и так оно и есть. Теперь свернем этот лист бумаги в цилиндр. Двухмерная поверхность цилиндра, согласно Гауссу, имеет две главные кривизны, проходящие в направлениях, перпендикулярных друг другу: первая кривизна относится к окружности и имеет величину 1/r, где r — это радиус основания цилиндра. Если r = 1, то эта кривизна также равна единице. Вторая кривизна проходит вдоль образующей цилиндра, которая представляет собой прямую линию. Кривизна прямой линии, очевидно, равна нулю, поскольку прямая — она и есть прямая. Гауссова кривизна цилиндра, как любого другого двухмерного объекта, равна произведению одной кривизны на вторую, которое в нашем случае равно 1×0 = 0. Таким образом, в понятиях собственной кривизны цилиндр представляет собой то же самое, что и лист бумаги, из которого он свернут, — он совершенно плоский. Нулевая собственная кривизна цилиндра обусловлена тем, что цилиндр можно сделать из листа бумаги, не растягивая и не деформируя его. Иными словами, измерения расстояний между любыми двумя точками на поверхности листа — вне зависимости от того, разложен ли лист на столе или свернут в трубочку, — дадут одинаковые результаты. Это значит, что геометрия и, следовательно, собственная кривизна листа бумаги остаются неизменными вне зависимости от того, плоский этот лист или свернутый.

Аналогично, если бы удалось сделать из цилиндра тор, соединив его концы вместе — также без растяжений и деформаций, — то внутренняя кривизна полученного тора все равно осталась бы равной внутренней кривизне цилиндра, то есть нулю. На практике, однако, сделать так называемый плоский тор — по крайней мере в двух измерениях — невозможно по причинам, которые будут обсуждаться далее (в четвертой главе). Но теоретически подобный объект (называемый абстрактной поверхностью) изготовить можно, и он столь же важен для математики, как и те объекты, которые мы называем реальными.

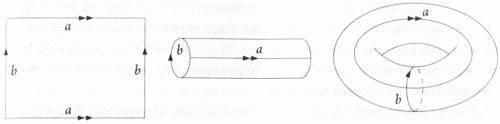
Рис. 2.4. Тороидальная (имеющая форму бублика) поверхность может быть совершенно «плоской» (имеющей нулевую гауссову кривизну), поскольку ее можно изготовить, сворачивая лист бумаги в трубку или цилиндр и затем соединяя концы полученного цилиндра

С другой стороны, сфера довольно существенно отличается от цилиндра или плоского тора. Рассмотрим, к примеру, кривизну сферы радиуса r. В этом случае кривизна одинакова по всей поверхности сферы, и ее можно определить как 1/r². Мы видим, что на поверхности сферы все направления эквивалентны, что явно неверно в случае цилиндра или бублика. Именно по этой причине не важно, как ориентирована сфера в трехмерном пространстве; маленький жучок, живущий на ее поверхности, скорее всего, не замечает пространственной ориентации сферы и все, что его беспокоит и дается ему в ощущениях, — это геометрия его локального двухмерного мира.

Наряду с Николаем Лобачевским и Яношем Бойяи Гаусс внес большой вклад в наше понимание абстрактного пространства, в частности для двухмерного случая, хотя он сам признавал наличие определенной путаницы в этой области. И все же, в конечном итоге, ни Гаусс, ни его коллеги не сумели полностью освободить наши представления о пространстве от евклидовых рамок. Гаусс выразил свое замешательство в письме, написанном им в 1817 году астроному Генриху Вильгельму Маттеусу Ольберсу: «Я все больше убеждаюсь, что необходимость нашей геометрии не может быть доказана, по крайней мере, человеческим рассудком и для человеческого рассудка. Может быть, в следующей жизни мы придем к взглядам на природу пространства, которые нам сейчас недоступны».[18]

Некоторые ответы были получены не в «следующей жизни», как написал Гаусс, а в следующем поколении благодаря усилиям и прекрасным способностям его студента Георга Фридриха Бернхарда Римана. Риман отличался слабым здоровьем и умер молодым, но за сорок лет своей жизни он смог перевернуть существовавшие представления о геометрии, а вместе с ними и представления о Вселенной. Риман ввел особую разновидность поля — набор чисел, соответствующий каждой точке пространства, пользуясь которым можно найти расстояние между двумя точками вдоль любой линии, которая их соединяет. Полученная информация, в свою очередь, может быть использована для определения степени искривленности пространства.

Проще всего мерить пространство в одном измерении. Все, что необходимо для измерения, например, прямой линии, — это линейка. Для двухмерного пространства, такого как пол большого танцевального зала, мы обычно берем две перпендикулярные линейки — одна из которых сопоставляется оси x, а вторая — оси y — и находим расстояние между двумя точками путем построения прямоугольного треугольника и применения теоремы Пифагора. В свою очередь, в трех измерениях нам необходимы три перпендикулярные линейки, соответствующие осям x, y и z.

В искривленных, неевклидовых пространствах все становится сложнее и интереснее, поскольку точно откалиброванные перпендикулярные линейки для измерения искривленного пространства уже не пригодны. Однако в этом случае для расчета расстояний мы можем использовать риманову геометрию. Подход, который мы применяем для расчета длины кривой, лежащей на искривленном многообразии, вам уже знаком: кривую представляют в виде ломаной, состоящей из касательных бесконечно малой длины, и затем берут интеграл вдоль всей линии, чтобы получить полную длину.

Сложность этого подхода обусловлена тем, что в искривленном пространстве длина каждого отрезка ломаной может изменяться при перемещении от одной точки многообразия к другой. Для того чтобы преодолеть эту трудность, Риман создал инструмент, известный как метрический тензор, дающий алгоритм для расчета длины отрезка касательной в каждой точке. В двух измерениях метрический тензор представляет собой матрицу 2×2, в n измерениях — матрицу n×n. Следует отметить, что этот новый подход к измерению, несмотря на всю важность нововведений Римана, по-прежнему основан на теореме Пифагора, только переформулированной для неевклидового пространства.