Теоретическая механика. Часть 1. Статистика - Страница 1
М.И. Бармин
Теоретическая механика
ЧАСТЬ 1. С Т А Т И К А
Краткий конспект лекций
по ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ с включением примеров решения типовых задач по всем темам курса
Санкт – Петербург
ВВЕДЕНИЕ
Данный конспект лекций составлен автором на базе анализа лекционных курсов для технологических специальностей ряда Вузов различных направлений.
Общенаучный курс теоретической механики , являющийся основой инженерных : деталей машин, теории механизмов и машин, сопротивления материалов и др. в настоящее время необоснованно сокращен в целом ряде Вузов страны. Данный конспект ориентирован на объем курса до 102 учебных часов.
В конспект включены как наиболее типовые экзаменационные вопросы, так и задачи по всем темам курса с подробным решением.
.
СТАТИКА
Лекция 1
Введение
Механика-наука о механическом движении материальных точек и абсолютно твердых тел и силовом взаимодействии их, а также и о состоянии их равновесия.
Материальная точка -тело, собственными размерами которого можно пренебречь по сравнению с размерами траектории его движения.
Траектория м.т. –линия, описываемая м.т. в процессе движения со временем «t».
Время «t» является независимой переменной, одинаковой для любых систем отсчета , таких как декартовы, полярные, естественные и др. системы координат, с которыми Вас знакомили в курсе Высшей математики и Физики, являющимся базой для классического курса теоретической механики.
Абсолютно твердое тело – материальное тело, обдадающее массой «m» – (не только как количество вещества в теле, но больше как мера инертности тела m= , где Р-вес тела, а g=9,81 м с -ускорение свободного падения), которое не деформируется ни при каких нагрузках и расстояние между двумя любыми точками аб. Т. Т. Всегда постоянно.
Классический курс теоретической механики разделяется на три крупных части:
СТАТИКА– изучает силовое взаимодействие аб. т. т. и случай их равновесия;
КИНЕМАТИКА-изучает перемещение точек и тел в отвлечении от сил и причин, вызывающих эти перемещения;
ДИНАМИКА– изучает механическое движение точек и тел с учетом силовых и кинематических факторов.
АКСИОМЫ СТАТИКИ
.1.
Если на тело не действуют никакие силы, то оно находится в состоянии равновесия.
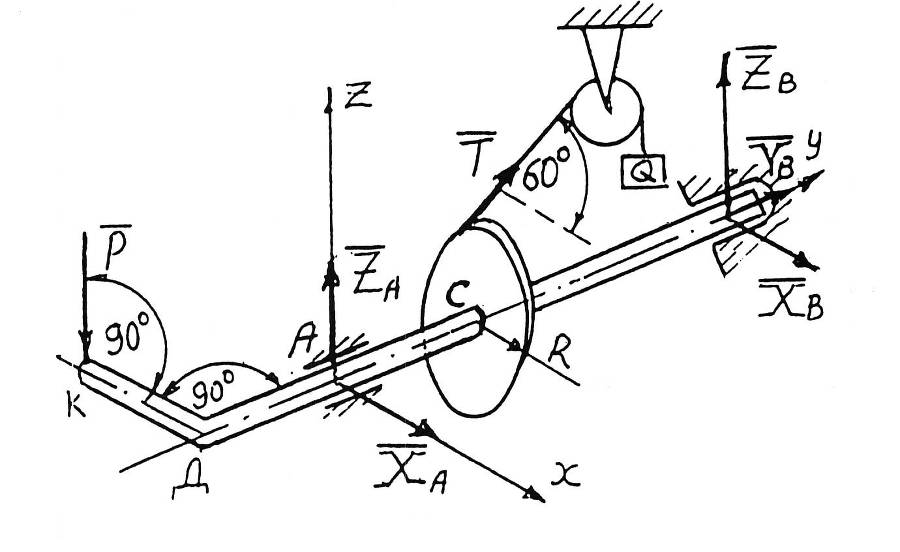
Сила F– мера взаимодействия тел, характеризуемая тремя факторами: величиной или F , измеряемой в Ньютонах (н) или килограммах силы (кГс) (1 кГс 9,8 н), направлением и точкой приложения. (рис. 1.1.).
Линия действия силы F (л. д.) – линия, вдоль которой действует сила.
Состояние равновесия тела – состояние покоя или равномерного прямолинейного движения его.
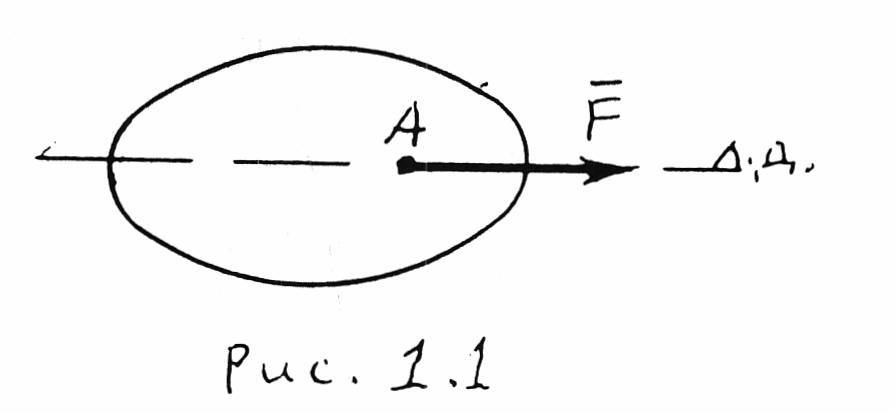
Под действием 2-х равных, противоположно направленных и действующих по одной линии действия (л. д.) сил тело находится в состоянии равновесия. (рис.1.2.).
Такая система сил называется взаимно уравновешенной.
От присоединения или отбрасывания взаимно уравновешенной системы сил состояние тела не изменяется.
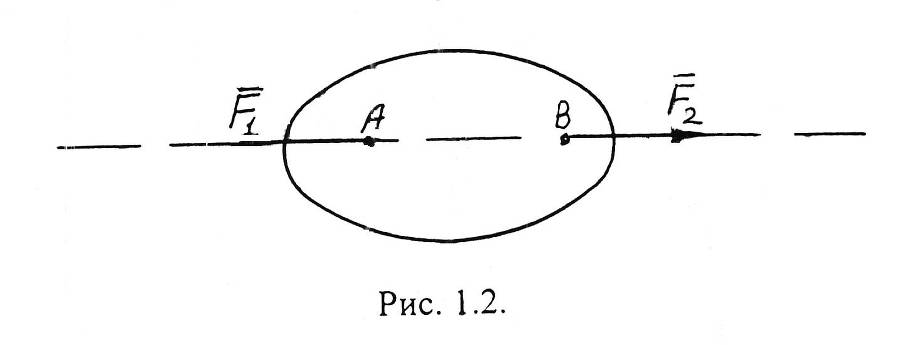
Следствие аксиомы 3: Точку приложения силы (точку А ) можно переносить вдоль линии действия тела, не нарушая его состояния.
Доказательство (рис. 1.3.):
Имеем тело и силу , приложенную в точке . В точке приложим = и взаимно уравновешенную ( = ), а затем отбросим взаимно уравновешенную систему сил и и получим (в) доказательство, т. к. = .
Понимать это важное на будущее следствие нужно так: для абсолютно твердого тела (аб. Т. т.) безразлично, будут ли его тянуть с силой F или с той же интенсивностью толкать силой F = F , лишь бы это было вдоль одной линии действия.
4. Равнодействующая 2-х непараллельных сил ( и ) находится по правилу сложения векторов графическим способом (рис. 1.4.). Т. е. = + равна диагонали параллелограмммма, построенного на этих силах как на сторонах и
приложена в точке пересечения этих сил (. А).
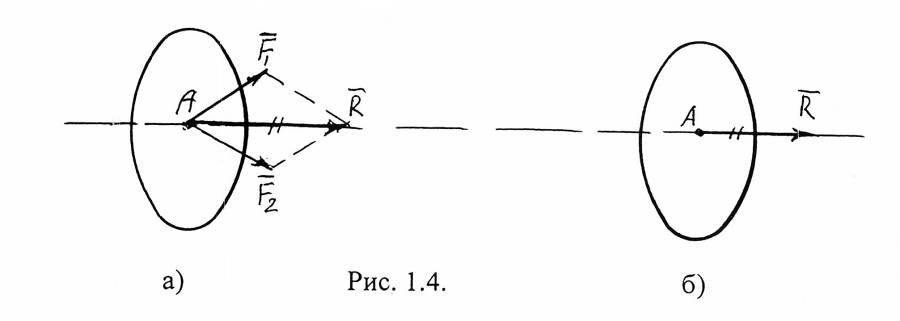
Равнодействующая (= + )– сила, оказывающая на тело такое-же воздействие, как и замененная ею система сил ( и ).
Примечание:
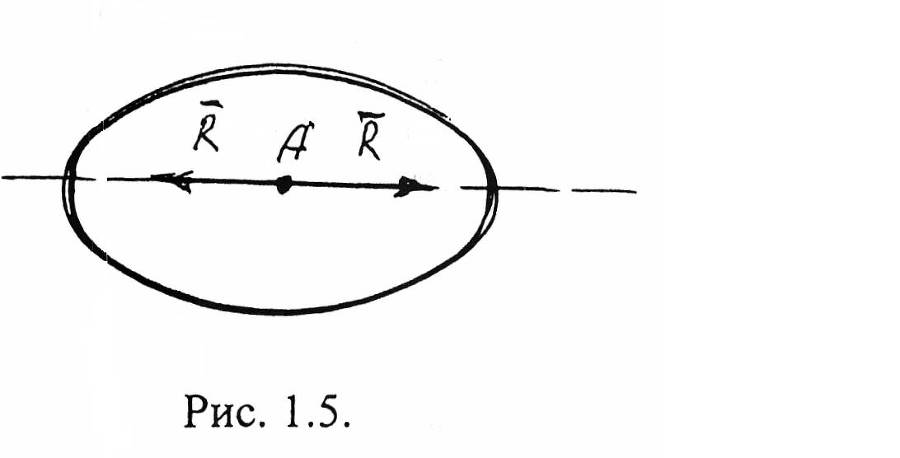
Сила ( = -), равная равнодействующей, но противоположно ей направленная по одной и той же л.д., называется уравновешивающей силой () (рис 1.5.)
5 Всякому действию соответствует равное и противоположно направленное противодействие.
На рис. 1.6. контактируют 2 тела в (.) А. Тело 1 воздействует на тело 2 силой, вызывая ответную реакцию, но несмотря на то, что эти силы н уравновешены, т. к. приложены к разным телам.

6. Равновесие твердого тела не нарушается при его затвердевании.
Например, стакан жидкости находится в равновесии и если эта жидкость, замерзнув в стакане, превратится в лед (аб. т. т.), то равновесие при этом не нарушится.
1.2. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
Связями называются тела, ограничивающие возможные перемещения рассматриваемого объекта (аб. т. т.). Например, для книги, положенной на стол этот стол и будет связью, т. к. он не дает книге падать вниз под действием силы тяжести P=m g.
Есть связи без трения – идеальные связи и есть связи с трением, которые более близки к реальным конструкциям и деталям машин (подшипники, подпятники и т. п.).
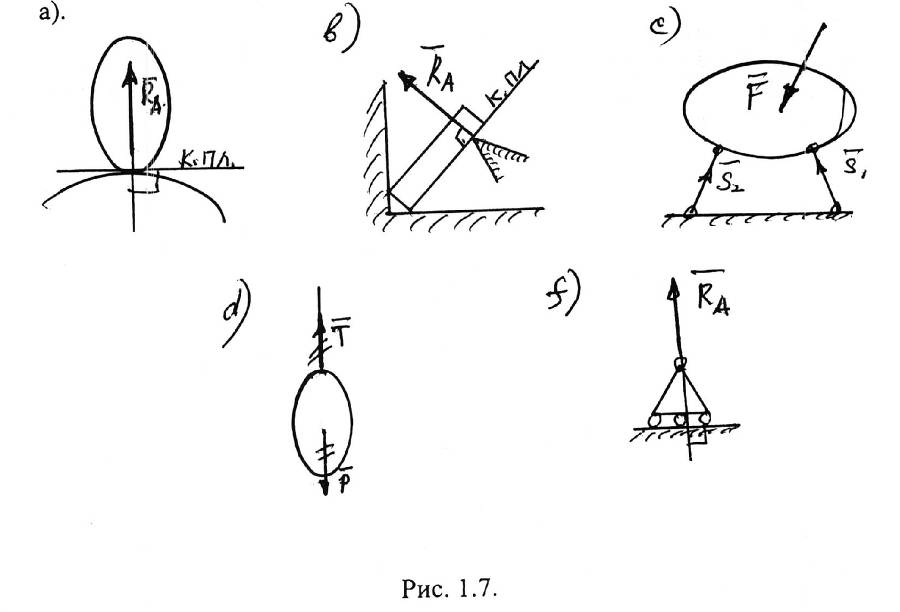
Реакция идеальной связи
всегда перпендикулярна к касательной плоскости, проведенной через точку соприкосновения 2-х тел (рис. 1.7, а).
Опора на угол, изображенная на рис. 1.7. (в) вызывает R , которая общей для плоскости бруса и вершины двухгранного угла ( . А) к. п. л.
Невесомые стержни от воздействия на них силовой нагрузки (рис. 1.7. с )испытывают усилия и , направленные по самим стержням.
Гибкие связи ( нити, веревки, канаты, тросы, цепи и т.д.) имеют реакцию [ () на рис. 1.7. (d) ], всегда направленную от объекта равновесия (о. р.).
Катковая (подвижная) опора [ рис. 1.7. (f)] имеет реакцию , всегда перпендикулярную плоскости опоры катков. Это типы связей, где реакция определена одним алгебраическим числом.
Есть типы связей, где реакция определяется 2-мя алгебраическими числами и для ее определения необходимо разложить ее на взаимно перпендикулярные составляющие [ рис. 1.8. (а) ] и , тогда величина , а направление вектора определяется направляющими косинусами углов с осями координат, например . К этим типам связей относят: