Статистика: конспект лекций - Страница 8
2) недостатки:
а) полученные данные всегда содержат ошибку;
б) о результатах наблюдения можно судить лишь с определенной степенью достоверности.
Вся совокупность единиц, из которых производится отбор, называется генеральной совокупностью. Часть единиц генеральной совокупности, отобранная в случайном порядке, составляет выборочную совокупность. Характеристиками генеральной и выборочной совокупности служат доля и средняя величина, а также дисперсия и среднее квадратическое отклонение. Средняя величина является характеристикой количественных признаков, а дол я – характеристикой альтернативных признаков.
Среднее значение признака генеральной совокупности называется генеральной средней, обозначается
Доля генеральной совокупности называется генеральной долей и обозначается р, доля выборочной совокупности называется выборочной долей и обозначается w. Численность генеральной совокупности обозначается N, а численность выборочной – n.
12. Ошибки выборочного наблюдения
Ошибка выборки – расхождение между характеристиками выборки и характеристиками генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования. Ошибка выборки состоит из ошибки регистрации и ошибки репрезентативности, которые бывают систематическими и случайными.
Систематические ошибки связаны с неправильной организацией и имеют тенденцию накапливаться. Случайные ошибки возникают вследствие того, что выборка недостаточно точно воспроизводит всю совокупность.
Ошибка репрезентативности обусловлена отличием структуры выборки от структуры генеральной совокупности. Чем больше единиц отобрано из генеральной совокупности, тем меньше ошибка выборки. Чем сильнее вариация, тем больше ошибка выборки.
Определение ошибки выборочной средней. При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

При бесповторном отборе она рассчитывается по формуле:

Определение ошибки выборочной доли. При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

где
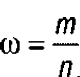
m — число единиц, обладающих изучаемым признаком; n — численность выборки.
При бесповторном способе отбора средняя ошибка выборочной доли определяется по формуле:

Предельная ошибка выборки Δ связана со средней ошибкой выборки μ отношением: Δ = t × μ.
При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.
Предельная ошибка выборки при бесповторном отборе определяется по формулам:
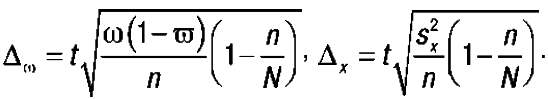
Предельная ошибка выборки при повторном отборе определяется по формулам:
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.