Софья Васильевна Ковалевская - Страница 72
В том же письме от 14 июня 1882 г. Вейерштрасс делится со своей ученицей «интересной и значительной математической новостью: ... профессор Линдеман в Фрей- бурге только что доказал, что я есть трансцендентное число [259], путем (что очень заинтересует Эрмита) оригинального обобщения основной теоремы, посредством которой Эрмит доказал, что е есть трансцендентное число. Простым следствием общей теоремы является следующее утверждение: если две действительные или комплексные величины а, Ь связаны между собой уравнением Ь=еа, то они обе никогда не могут быть алгебраическими числами, за исключением случая,

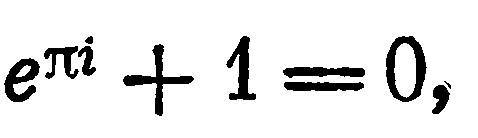
которое не могло бы удовлетворяться, если бы я i было алгебраическим.
Вейерштрасс стал думать над теоремой Линдемана и в следующем письме Ковалевской, от 15 июля 1882 г., написал, что работа Линдемана о числе я содержит правильные результаты, но вначале «они были основаны на ложно понятой теореме и не доказаны Линдеманом достаточно строго и теперь» [125, с. 237]. Сам Вейерштрасс, используя предложения, развиваемые Эрмитом «в его красивой работе об экспоненциальных функциях», пришел к вполне строгому и несложному доказательству лин- демановской теоремы.
Теоремы о трансцендентности в и я долго привлекали внимание математиков. Эрмит был доброжелателен в оценке работ других авторов, восхищался красивыми результатами, радовался, если какой-нибудь математик развивал дальше его идеи. В этом отношении интересно письмо (1893 г.) Г. Минковского Д. Гильберту, получив-
261
тему новое изящное доказательство трансцендентности е и я: «Час назад я получил твою заметку о е и я...и мне остается только выразить тебе мое искреннее и сердечное удивление... Я живо представляю себе оживление Эрмита, вызванное чтением твоей статьи. Насколько я знаю старика, я не удивлюсь, если в ближайшем будущем он сообщит тебе о своей радости, что он все еще способен испытывать наслаждение от такой работы» [255, с. 59].
Доброжелательность Эрмита к Ковалевской в первый период их переписки, в 1884 г., выражалась в проявлении интереса к ее преподавательской деятельности. В письме от 27 января 1884 г. он говорит по поводу ее курса уравнений с частными производными: «Точная теория, основанная на принципах Вейерштрасса, уравнений с частными производными, которую Вы, сударыня, излагаете в Стокгольмском университете, является очень важным и трудным вопросом. Вы окажете также слушателям этого университета огромную услугу, излагая им то, чего они не нашли бы ни в какой другой работе, кроме лекций Якоби» [77, с. 666].
А в письме от 8 марта 1884 г. Эрмит, изложив Ковалевской некоторые соображения по поводу мероморфных решений уравнения Лапласа, а также приведения гиперэллиптических интегралов, добавляет: «Эти подробности недостойны Вас, сударыня, только зная Вашу доброту и зная также, что Вы посвящаете себя трудоемкой работе тщательно приготовлять Ваши лекции, я позволяю себе сообщить их Вам» [77, с. 656].
В 1888 г. основной темой переписки Эрмита и Ковалевской была подготовка Софьей Васильевной задачи на премию Бордена. Она послала результаты своих исследований в Парижскую академию наук, однако ее не удовлетворяло ее изложение, о чем она написала Эрмиту. Тот ответил ей в письме от 11 июня 1888 г., что она сможет осенью прислать новую редакцию: у академиков вакации, и комиссия по премии не приступит к работе раньше октября. Вместе с тем Эрмит сообщает, что еще два мемуа- ра присланы на конкурс, один из Парижа, другой из Бреста, но кто их авторы, он не знает.
Далее Эрмит пишет в высшей степени любезные слова: «Не будучи удостоенным чести быть среди судей конкурса, я буду, Сударыня, одним из Ваших читателей, жаждущих узнать прекрасные и важные результаты, к которым Вы пришли в знаменитом вопросе и которые меня в выс¬
262
шей степени интересуют. Мне будет приятно "подбирать колосья со сжатого Вами поля. Я уже мечтаю об Изучении частных случаев, в которых Ваши гиперэллиптические интегралы приводятся к эллиптическим функциям, подобно тем примерам, которые дали Якоби и другие» [77, с. 675],
Летом 1888 г. Ковалевская была в Париже. Письмо Эрмита от 19 июня содержит приглашение Ковалевской на обед, на который ожидаются Пикар с женой (дочерью Эрмита) и детьми. Раньше госпожа Эрмит не приглашала к себе Ковалевскую, на что та немного обижалась. Теперь Ковалевская входила в их тесный семейный круг.
Когда Вейерштрасс узнал о том, что его ученица познакомилась с Эрмитом, он посоветовал ей также познакомиться с другими французскими математиками, из которых наиболее интересными для Ковалевской он считал младших: П. Аппеля, Э. Пикара, А. Пуанкаре. При этом он говорит: «Пуанкаре, по моему мнению, наиболее способный из всех к математическим исследованиям. Только бы он не рассеял свой исключительный талант и дал созреть своим исследованиям. Теоремы об алгебраических уравнениях с двумя переменными и линейных дифференциальных уравнениях, которые он дал в «Comptes rendus», действительно производят впечатление» [125, с. 231].
О созвездии трех математиков написал Ковалевской и Эрмит: «Г. Пикар работает вовсю и печатает замечательные работы, как, впрочем, и г. Аппель, и г. Пуанкаре, и меня с чрезвычайной горечью упрекают, что я их слишком хвалю» [77, с. 656].
Вероятно, Эрмит имел в виду мнение Вейерштрасса по поводу его питомцев, которое он высказал не только одной Софье Васильевне. Ей же он писал 11 апреля 1882 г.: «Обратила ли Ты внимание на последние работы Пуанкаре? Это, во всяком случае, крупный математический талант». Однако Вейерштрасс сожалеет, что «Академия является слишком манящей целью для молодых французских исследователей. Каждую неделю представлять в «Comptes rendus» статью, действительно ценную,— это все-таки невозможно. Даже талантливый Пикар расточает свой талант таким образом, а Эрмит слишком поощряет эту беспокойную погоню за внешним успехом» [125, с. 230].
Пикар и Аппель и особенно Пуанкаре были очень плодовитыми авторами [260, 261]. У Пуанкаре к концу жизни была опубликована 561 работа. Все трое стали членами
263
Парижской академии наук, а Пуанкаре, кроме того, в 1908 г. был избран во Французскую академию (в числе 40 бессмертных!) за свои книги по философии науки.
К 1882 г., когда Ковалевская познакомилась с Пуанкаре, он еще не имел прославивших его исследований по небесной механике и по фигурам равновесия вращающейся жидкости. Но у него уже был опубликован ряд статей по алгебраическим уравнениям, линейным дифференциальным уравнениям с алгебраическими коэффициентами и фуксовым функциям. В ноябре 1881 г. вышла первая часть его знаменитого мемуара «О кривых, определяемых дифференциальными уравнениями», вторая часть появилась в августе 1882 г. [262]. Ковалевская настолько внимательно изучала эти мемуары, что, когда в 1883 г. был решен вопрос о ее приезде в Стокгольм, она предложила в качестве одного из математических курсов, который она могла бы прочитать, исследования Пуанкаре о кривых, определяемых дифференциальными уравнениями. Когда Ковалевская бывала в Париже, она обязательно навещала Пуанкаре и огорчалась, если его не было в городе, так как считала разговоры с ним очень интересными.
Эмиль Пикар был любимым учеником Эрмита, а в 1881 г. стал его зятем. По словам его биографа [263], Пн- кар обладал независимым и твердым характером и прекрасной памятью. Редко он употреблял целый день на занятия одной математикой: он много читал по истории а философии, искусству и археологии. Много путешествовал, был в Египте, США, в Норвегии — к 100-летию Абеля. Он написал много книг, в том числе по философии науки, по истории математики XIX в., в которой упоминает имя Ковалевской [267], и четырехтомный курс анализа. В 1877 г. появились две первые статьи Пикара — по теории поверхностей, а в 1879 г. он начал печатать свои статьи о целых функциях, содержащие знаменитые теоремы Пикара.