Разумное распределение активов. Как построить портфель с максимальной доходностью и минимальным риск - Страница 4

Подбрасывание монеты также вводит разницу между средней доходностью актива и годовой доходностью (доходностью в годовом исчислении). Кто-то из вас спросит, почему доходность при подбрасывании монеты составляет не 10 %, а 8,17 %, поскольку среднее значение доходности в +30 % и –10 % равно +10 % (30 минус 10, деленное на 2). Средняя доходность – это просто среднее значение отдельной доходности за один год. Годовая доходность – более тонкое понятие; это доходность, которую вы должны получать каждый год, чтобы уравновесить различную доходность за ряд лет. Если вы владеете акциями, стоимость которых удваивается (вы получаете на них 100 % дохода) в первый год, а затем на следующий год ваш убыток составляет 50 %, то вы имеете нулевую годовую доходность. Если вначале цена ваших акций составляла $10 за акцию, то к концу первого года она составит $20, а к концу второго года – снова $10. Вы не заработали, и тем не менее средняя доходность составляет 25 % (среднее значение +100 % и –50 %). Ваша годовая доходность равна нулю. Годовая доходность и средняя доходность – определенно не одно и то же. При подбрасывании монеты получаем среднюю доходность в 10 % и годовую доходность в 8,17 %. Доходность в годовом исчислении всегда меньше, чем средняя доходность. Если при подбрасывании монеты в половине случаев вы получаете доход в –10 %, а в половине – +30 %, то это будет то же самое, что и получение дохода в размере 8,17 % ежегодно. Вы оплачиваете свои счета из годового, а не из среднего дохода. Вот почему первый так важен.

Рис. 1.1. Вероятность подбрасывания монеты дядюшкой Фредом

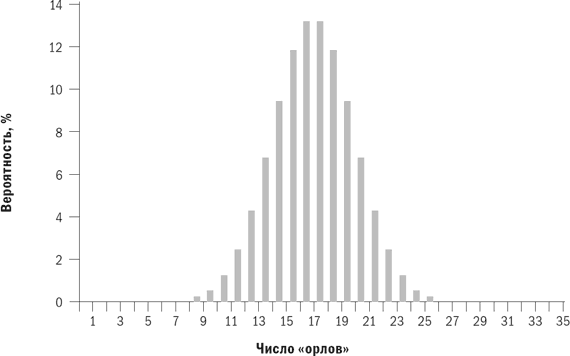
Подбрасывание монеты дядюшкой Фредом может казаться странным способом, однако он мало отличается от выбора, перед которым стоит большинство инвесторов – между безопасностью счетов денежного рынка или казначейских векселей и рискованностью обыкновенных акций. Второй вариант предлагает почти наверняка превосходный результат, но какой ценой: небольшая вероятность получения более низкого результата и ежегодное леденящее душу подбрасывание монеты дядюшкой Фредом. Однако действительно беспокоить должен вариант с депозитными сертификатами, имеющими доходность 3 %: выбрав его, вы почти наверняка проживете свои золотые годы в бедности.

Я сознательно привел этот пример с подбрасыванием монеты дядюшкой Фредом – его легко понять, и он довольно четко отражает приблизительную доходность и риски вложения в обыкновенные акции. Например, доходность обыкновенных акций за период с 1926 по 1998 г. составляла 11,22 % годовых, то есть примерно в том же диапазоне, что и при подбрасывании монеты. Что более важно, «рискованность» подбрасывания монеты и обыкновенных акций практически одинакова. Вскоре я объясню, как точно измерить эту рискованность. Подбрасывание монеты – это удобное символическое представление рисков и доходности обыкновенных акций. Это также хороший способ понять поведение портфелей со всевозможными классами активов.

Вы только что узнали об одном из фундаментальных законов инвестирования: в итоге вы получаете компенсацию за то, что рискуете. И наоборот, если вы стремитесь обезопасить свои инвестиции, то ваш доход будет низким. Опытные инвесторы понимают, что вознаграждение и риск сложно связаны между собой. Один из самых верных признаков инвестиционного мошенничества – вам предлагают слишком высокую доходность с низким уровнем риска.

Рассмотрим более сложный способ расчета доходности инвестиций, чем подбрасывание монеты. Скажем, вы инвестировали средства в актив «А» (неважно, что он собой представляет). В течение последовательных восьми лет вы будете ежегодно получать следующую доходность:

• год 1: 20 %;

• год 2: 0 %;

• год 3: 10 %;

• год 4: –10 %;

• год 5: 30 %;

• год 6: 15 %;

• год 7: 10 %;

• год 8: 5 %.

Какова ваша доходность от инвестиции в актив «А»? В году 1 доходность составила 20 %; поэтому умножьте стоимость своего актива на 1,2. В году 2 вы умножаете ее на 1,0. В году 3 вы умножаете ее на 1,1, и в году 4, получая убыток 10 %, вы умножаете стоимость актива на 0,9. Таким образом, через восемь полных лет окончательная стоимость вашего актива рассчитывается как:

Таким образом, если актив «А» стоил $10 в начале периода, то сейчас он стоит в 2,051 раза больше своей начальной стоимости, то есть $20,51. Суммарный доход за восемь лет составляет 105,1 %. (Пусть вас это не смущает; помните, что рост на 50 % означает, что вашу начальную сумму нужно умножить на 1,5 и что рост на 100 % означает умножение на 2.) Средняя доходность (среднее арифметическое значение доходности) за восьмилетний период, рассмотренный в примере выше, составляет 10 %. Однако мы знаем, что на самом деле важна годовая доходность (то есть доход, который потребуется получать каждый год, чтобы иметь такой же результат). Как ее рассчитать? Если вы знакомы с электронными таблицами, то это не займет много времени: все пакеты электронных таблиц имеют обширные возможности для проведения финансовых расчетов. Если вы не имеете опыта работы с электронными таблицами, то проще всего выполнить расчеты с помощью финансового калькулятора. Рекомендую изучить функции расчета аннуитетных платежей – это умение необходимо при планировании пенсионных выплат, расчета выплат по ссудам и т. д. Финансовые калькуляторы также поддерживают статистическую функцию, позволяющую быстро рассчитать риск инвестиций исходя из доходности за ряд периодов. Введем в калькулятор значения для расчета аннуитетных платежей и выясним, что годовая доходность для примера, рассмотренного выше, равна 9,397 %. Вас не должно удивлять, что она несколько ниже средней доходности, равной 10 %, поскольку годовая доходность всегда ниже средней доходности.

Теперь мы готовы рассчитать риск актива «А». Для этого рассчитывается стандартное отклонение, служащее мерой разброса множества чисел. Расчеты можно произвести вручную, однако это чересчур утомительно. Обычно они производятся с помощью электронных таблиц или финансового калькулятора. В приведенном выше примере расчета доходности за восьмилетний период стандартное отклонение доходности составило 11,46 %.

Что делать со стандартным отклонением? Прежде всего, следует ознакомиться с ним как с мерой риска. Обычно стандартное отклонение доходности для различных классов активов таково:

• денежный рынок (наличность): 2–3 %;

• краткосрочные облигации: 3–5 %;

• долгосрочные облигации: 6–8 %;

• акции компаний США (консервативные активы): 10–14 %;

• акции компаний США (агрессивные активы): 15–25 %;

• акции иностранных компаний: 15–25 %;

• акции компаний развивающихся стран: 25–35 %.

Рейтинговые службы практически всех взаимных фондов приводят в своих отчетах величины стандартного отклонения. Morningstar (www.morningstar.com), компания, занимающаяся сбором информации и анализом деятельности взаимных фондов, указывает стандартные отклонения годовой доходности за предыдущие 3, 5 и 10 лет. В некоторых случаях вы можете иметь доход только за один или два года. Тогда стандартное отклонение годовой доходности можно определить, умножив стандартное отклонение квартальной доходности на 2 или стандартное отклонение месячной доходности на 3,46. Каждый раз, когда продавец или брокер пытается продать вам какую-либо ценную бумагу, узнайте у него величину стандартного отклонения годовой доходности (или ожидаемую величину отклонения, если идет речь о первичном размещении). Если ответа нет, даже не думайте о покупке. Если вашему брокеру незнакомо понятие стандартного отклонения доходности, найдите другого.

Что в действительности означает стандартное отклонение? Оно означает, что две третьих всего времени годовая доходность актива будет находиться между одним стандартным отклонением выше и одним стандартным отклонением ниже среднего значения. В случае с активом «А» это означает, что две третьих всего времени этот показатель будет находиться между значениями –1,46 % (10 минус 11,46) и 21,46 % (10 плюс 11,46). На рис. 1.2 я изобразил обратную сторону актива «А». Можно видеть, что существует один шанс из шести получить убыток, превышающий 1,46 %. Существует один шанс из 44 получить убыток, превышающий 12,92 % (на два стандартных отклонения меньше среднего), и один шанс из 740 получить убыток, превышающий 24,38 % (на три стандартных отклонения меньше среднего).