Пятьсот двадцать головоломок - Страница 63
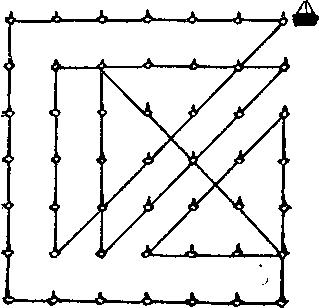
405. На рисунке показано, каким образом военный корабль может потопить 49 судов за 12 прямых курсов, закончив движение в той же точке, откуда начал. Двигайтесь вдоль каждой прямой до того места, где он меняет направление.
[Доказано, что можно соединить все точки, расположенные в виде квадрата n× n, непрерывным путем, состоящим из 2 n- 2 отрезков прямой, для всех n >2. Случай n= 3 представляет собой хорошо известную головоломку, которую большинству решить не удается, поскольку те, кто решает, не всегда догадываются продолжить отрезки за пределы квадрата. 5 × 5 — это наименьший квадрат, в котором линия из 2 n- 2 отрезков может не выходить за его пределы.
Можно построить замкнутый путь (у такого пути концы совпадают, как в приведенной выше головоломке) из 2 n- 2 отрезков для всех квадратов со стороной, большей 3. Квадрат 7 × 7 представляет собой наименьший квадрат с нечетной стороной, для которого существует замкнутый путь из 2 n- 2 отрезков, не выходящий за пределы данного квадрата. (Наименьший квадрат с четной стороной, для которого можно нарисовать подобный путь, равен 6 × 6.)
Приведенное здесь Дьюдени решение имеется в книге Сэма Лойда «Cyclopedia of Puzzles» как решение одной из его головоломок. Лойд говорит, что он впервые опубликовал эту головоломку в 1908 г., и отзывается о данном решении как об «удивительно трудном трюке». Позаимствовал ли Лойд свою головоломку у Дьюдени или наоборот, еще не установлено.
Обратите внимание на то, что это решение для случая 7 × 7 является одновременно решением задачи о замкнутом «пути ферзя» на шахматной доске 7 × 7 за 2 n- 2 ходов. Замкнутый путь ферзя за 2 n- 2 ходов возможен также на любой доске со сторонами, большими 7. Замкнутый путь ферзя за 14 ходов на обычной доске 8 × 8 был впервые найден Сэмом Лойдом, который считал эту задачу одной из лучших своих головоломок.
Число 2 n- 2 является необходимым также для любой квадратной доски. — М. Г.]

406. Из дома Hдо любой из точек, расположенных к северу или к востоку от него, можно добраться лишь одним путем. Поэтому я в этих точках поставил цифру 1. Теперь возьмем второй столбец и заметим, что существуют 3 пути, ведущие во вторую снизу точку, 5 — в следующую, 7 — в следующую за ней и т. д., причем при переходе в очередную расположенную выше точку число путей увеличивается на 2. То же самое применимо и ко второй снизу строке. Выпишем везде соответствующие цифры. Далее, до центральной точки можно добраться 13 путями, поскольку мы можем к ней подойти или из точки снизу (5 путей), или из точки слева (5 путей), или из точки слева внизу по диагонали (3 пути), что в сумме и даст 13 путей. Таким образом, все, что нам осталось сделать,- это выписывать по очереди в каждой точке сумму трех чисел, расположенных в ближайших точках, из которых можно непосредственно попасть в данную. Отсюда мы и получим, что общее число путей, ведущих из Hв C, равно 321.
407. На рисунке показано, как лучше всего разрезать сеть. Нетрудно видеть, что 8 разрезов от Aдо Bделят сеть на 2 части.

408. Можно заметить, что каждый участок соединен с остальными четным числом мостов (2, 4 или 6); исключение составляют участки Cи L, в которые ведут по 3 моста (нечетное число). Следовательно, чтобы пройти по каждому мосту один и только один раз, необходимо начинать и заканчивать маршрут в Cи L, где как раз и расположены дома наших двух приятелей. Так, отправляясь из C, мы можем двигаться по следующему маршруту: C, G, F, C, B, A, D, H, E, I, H, J, K, L, M, G, I, F, B, E, F, I, L.

409. Решение ясно из рисунка.
410. Фразу HERE LIES JOHN RENIE можно прочитать 45 760 способами (или, если разрешается перемещаться от одной буквы к следующей и по диагонали, 91 520 способами), поскольку, добравшись до углового I, мы обязаны сместиться назад по диагонали к ближайшему Е. За недостатком места здесь не приводятся детали решения. Единственная дополнительная информация о камне заключается в окончании фразы: «...который умер 31 мая 1832 г. в возрасте 32 лет».

411. На рисунке показан путь, удовлетворяющий всем заданным условиям.
412. Наикратчайший путь в ABCHCDEIEFGBHDIHGIFAG. Таким образом, инспектор проделает путь в 211 км, проехав по двум коротким дорогам CHи EIдважды.
413. Существует 2501 маршрут от Bдо D, а именно:
| Количество | Число | Число | |
| участков | маршрутов | вариаций | |
| 1 | 1 | 2 | 2 |
| 2 | 1 | 9 | 9 |
| 3 | 2 | 12 | 24 |
| 4 | 5 | 18 | 90 |
| 5 | 4 | 72 | 288 |
| 6 | 14 | 36 | 504 |
| 8 | 22 | 72 | 1584 |
| 2501 |
Достаточно рассмотреть маршруты от Bдо D. Маршрут, состоящий из 1 участка, ведет прямо в D. Маршрут из 2 участков есть CD. Маршрутами из 3 участков будут CBDи DCD. Пятью маршрутами из 4 участков являются DBCD, DCBD, CBCD, CDCDи CDBD. У каждого из этих маршрутов есть вариации, связанные с выбором конкретных участков, и число таких вариаций одинаково для любого маршрута, содержащего данное количество участков. Маршрутов с семью участками не существует.
414. Число различных путей равно 264. Эта головоломка довольно трудна, но недостаток места не позволяет мне показать наилучший метод подсчета всех маршрутов.
415. Существует 60 маршрутов, следуя по которым миссис Симпер могла бы посетить каждый город по одному и только по одному разу, закончив путь в H, если считать различными маршруты, отличающиеся только направлением. Однако если леди должна избежать тоннелей между Nи O, а также между Sи R, то можно обнаружить, что число различных маршрутов сокращается до 8.
Если это заинтересует читателя, то он может попытаться самостоятельно определить все 8 маршрутов. Поступив таким образом, он обнаружит, что маршрутом, удовлетворяющим всем условиям, то есть не включающим в себя два тоннеля и задерживающим визит в Dкак можно дольше, окажется маршрут HISTLKBCMNU QRGFPODEAH. Он, несомненно, и будет наилучшим маршрутом.

416. На рисунке показан маршрут длиной 76 км, состоящий из 16 прямолинейных участков и не охватывающий только 3 города. Эта головоломка не простая, ее решение можно найти только после большого числа проб и ошибок.
[Милли улучшил решение, найдя 76-километровый путь, состоящий из 16 отрезков и не захватывающий только одингород. По-видимому, это наилучшее возможное решение. Читатель может попытаться его найти. — М. Г.]
417. На рисунке, где для большей ясности опущены неиспользованные дороги, показаны маршруты всех 5 автомобилей. Все маршруты не имеют общих участков и не пересекаются. Хотя точного правила для решения головоломок такого рода указать нельзя, тем не менее, внимательно подумав, мы обычно можем справиться со встретившимися здесь трудностями. Например, уже было показано, что если соединить Aс Aпо вертикали, то C, Dи Eокажутся отрезанными друг от друга. Вскоре выясняется, что путь из Aдолжен обойти слева верхнее D, а затем пройти справа от C. Таким образом, становится очевидным путь из Dв Dи из Bв B. Остальное закончить уже легко.