Путешествие к далеким мирам - Страница 93
Б. Период обращения спутника
Время, за которое спутник совершит один полный оборот вокруг Земли, равно, очевидно, длине пути за оборот, деленной на круговую скорость:

(Т — так называемый сидерический, или звездный, период обращения).
Но вследствие чего



Подстановка значений R и g0 дает следующую довольно точную для приближенных расчетов формулу:
| Высота Н в км | Период обращения спутника Т в сек |
|---|---|
| 0 | 5 070 (1,4 часа) |
| 255 | 5 400 (1,5 часа) |
| 1 000 | 6 340 (1,76 часа) |
| 1 670 | 7 200 (2 часа) |
| 35 800 | 86 400 (24 часа) |
| 384 000 | 2,36·106 (27,3 суток) |
III. СКОРОСТЬ ОТРЫВА (ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ)
Скорость отрыва (или параболическая скорость) есть та скорость, которая должна быть сообщена телу у поверхности Земли, чтобы полностью преодолеть поле земного тяготения — удалить тело в бесконечность.
Величина скорости отрыва Vотр. определяется тем, что кинетическая энергия тела должна в этом случае в точности равняться работе преодоления поля тяготения; с помощью высшей математики получаем:

то есть работа полного преодоления поля земного тяготения равна работе поднятия тела при постоянном ускорении силы тяжести, равном его значению у земной поверхности g0, на высоту земного радиуса R.
Так как √g0R есть круговая скорость, то скорость отрыва Vотp. в 1,41 раза больше круговой скорости:
| Высота Н в км | Скорость отрыва Уотр. в км/сек |
|---|---|
| 0 | 11,2 |
| 300 | 10,9 |
| 1 000 | 10,4 |
| 1 670 | 9,9 |
| 35 800 | 4,3 |
| 384 000 | 1,42 |
IV. ОБЩИЙ ЗАКОН ДВИЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ В ПОЛЕ ТЯГОТЕНИЯ ОДНОГО НЕБЕСНОГО ТЕЛА
Примеры движения по кругу или по параболе, о которых шла речь выше, являются лишь частными случаями движения тела в поле тяготения небесного тела большой массы. Как известно из небесной механики, в общем случае орбитой такого движения является одна из кривых второго порядка (так называемых конических сечений): круг, эллипс, парабола или гипербола. Общий закон этого движения дается следующей формулой (так называемое уравнение живых сил, упрощенное для случая космического корабля, то есть тела небольшой массы):

или где V — скорость движения тела массы пренебрежимо малой по сравнению с М;

М — масса небесного тела;
f — гравитационная постоянная;
L — расстояние до центра тяжести небесного тела;
а — большая полуось орбиты;
g0 — ускорение силы тяжести на поверхности небесного тела на расстоянии R0 от его центра.
Как видно из формул, характер орбиты зависит лишь от величины, но не направления скорости V. Различные типы орбит соответствуют следующим частным случаям:
а) а = ∞,

орбита — парабола;
б) а > ◯, V < Vпараб., орбита — эллипс;
в) L = а, V = Vкруг =
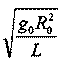
частный случай эллиптической орбиты — круговая;
г) а < ◯, V>Vпараб., орбита — гипербола (V гиперб.).
По какой орбите будет двигаться космический корабль, летящий на расстоянии 100 000 км от центра Земли со скоростью 5 км/сек?
По формуле откуда a ≈ — 24 000;

так как а < ◯, то V = Vгиперб., орбита — гипербола.
V. ЭЛЛИПТИЧЕСКИЕ ОРБИТЫ
Наиболее важными для астронавтики являются эллиптические орбиты, по которым будут двигаться не только все новые искусственные спутники Земли, но чаще всего и космические корабли. Полет по гиперболической орбите — дело более отдаленного будущего (советская космическая ракета, запущенная 2 января 1959 года, летела в поле земного тяготения по гиперболе, а вокруг Солнца движется по эллипсу).
Формулы расчета эллиптических орбит могут быть получены из приведенного выше уравнения живых сил путем упрощений;
для движения вокруг Солнца:
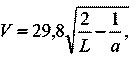
где V — в км/сек,
L,a — в астрономических единицах (1 а. е. — расстояние от Земли до Солнца, равное примерно 150·106 км);
для движения вокруг Земли:

где V — в км/сек,
L, а — в радиусах земного шара.
1. Какова должна быть скорость корабля при взлете с Земли для того, чтобы он смог совершить полет на Меркурий по наивыгоднейшей, то есть касательной, эллиптической орбите?

В этом случае
и
Так как круговая скорость Земли равна 29,8 км/сек, то, очевидно, кораблю при взлете нужно сообщить скорость против направления движения Земли по орбите, равную 29,8 — 22,3 = 7,5 км/сек.
2. Какова будет скорость корабля в упомянутой выше задаче на орбите Меркурия?
В этом случае L2=0,387 а. е., а = 0,6935 а. е., вследствие чего
Так как круговая скорость Меркурия равна 47,9 км/сек (это можно проверить и так — она равна круговой скорости Земли, деленной на √0,387, то есть то корабль будет двигаться быстрее Меркурия на величину 57,5 — 47,9 = 9,6 км/сек.

3. Какова должна быть взлетная скорость ракеты, доставляющей о Земли груз на искусственный спутник, находящийся на суточной орбите (высота 35 800 км), если сопротивление воздуха не учитывать? Какова будет скорость этой ракеты на орбите спутника?