Плач математика. Эссе о преподавании математики в школе (ЛП) - Страница 8
Этот вирус атакует математику в самое сердце, создавая иллюзию, будто именно на уроке геометрии школьники знакомятся с математическим рассуждением, и тем самым разрушает саму суть творческого рационального мышления, отравляя учеников в стремлении к этому занимательному и красивому предмету, навсегда калеча их способность мыслить о математике естественным и интуитивным путем.
Механизм, стоящий за этим, тонок и изощрен. Жертва-ученик сначала оглушается и парализуется потоком бессмысленных определений, положений и значков, а затем медленно и болезненно отлучается от естественного интереса и интуиции о геометрических формах и их закономерностях систематической пропагандой корявого языка и искусственного формата так называемого «формального геометрического доказательства».
Скажем прямо и без метафор: урок геометрии есть наиболее эмоционально и ментально деструктивная компонента всей математической программы от первого класса и до последнего. Другие математические курсы могут спрятать прекрасную птицу или посадить ее в клетку; лишь на уроке геометрии ее подвергают бездушным пыткам. (Нет, видимо, я еще не готов говорить без метафор.)
Здесь систематически подрывается интуиция ученика. Доказательство, математическое рассуждение есть произведение искусства, поэма. Ее цель — удовлетворить. Красивое доказательство призвано объяснять, и объяснять ясно, глубоко и элегантно. Хорошо написанное, проработанное рассуждение должно чувствоваться холодными брызгами и вести лучом маяка — освежать дух и освещать ум. Оно должно очаровывать.
В том, что сходит за доказательство на уроке геометрии, нет ничего очаровательного. Школьникам дают негибкий, догматический формат, в котором они должны производить так называемые «доказательства» — формат настолько непотребный и неподходящий, как, например, требование от детей, желающих высадить сад цветами, называть их цветы латинскими видом и родом.
Рассмотрим примеры этого безумия. Начнем с рисунка двух пересекающихся прямых:

На первом шаге рисунок следует замутить излишними обозначениями. Нельзя говорить о двух пересекающихся прямых: им следует дать вычурные обозначения. Не просто «прямая 1» и «прямая 2», или a и b. Мы должны, в соответствии с требованиями школьной геометрии, выбрать произвольные ненужные точки на этих прямых и называть эти прямые в соответствии со специальной «системой обозначения прямых».

Теперь мы будем называть их AB и CD. Боже упаси забыть надчеркивание: запись AB обозначала бы длину отрезка (во всяком случае, как это делается сейчас
). Ничего, что эта система бессмысленно усложнена, просто научитесь ею пользоваться. Теперь начинается собственно доказательство, обычно предваряемое каким-нибудь абсурдным названием, например,ТЕОРЕМА 2.1.1
Пусть AB и CD пересекаются в точке P.
Тогда ∠APC ≌ ∠BPD
.
То есть — что углы одинаковы. Да пересекающиеся прямые симметричны, ради всего святого! И, как будто этого мало, это очевидно верное утверждение должно быть «доказано»:
Доказательство.

Вместо остроумного и интересного рассуждения, написанного человеческим существом на одном из естественных языков Земли, нам предлагается это гнетущее, бездушное, бюрократическое заполнение бланка. И какого слона удалось раздуть из мухи! Мы что, на самом деле хотим показать, что самоочевидное наблюдение требует такого огромного введения? Честно: вы его прочитали или нет? Нет. Кто станет это читать?
Такой вывод столь элементарного утверждения заставляет людей сомневаться в собственной интуиции. Подвергая сомнению очевидное, настаивая на том, чтобы оно было «строго доказано» (как будто вышеприведенное доказательство строгое!), ученику как бы говорят: «Твоя интуиция и твои идеи сомнительны. Ты должен говорить и думать по-нашему».
В математике, без сомнения, есть место формальному доказательству. Но место ему не в первом введении ученика в предмет математического рассуждения. Позвольте ему сперва ознакомиться с некоторыми математическими объектами, понять, чего от них можно ожидать, перед тем, как вы начнете все формализовать. Строгое формальное доказательство необходимо только в кризисной ситуации, когда ваши воображаемые объекты начинают вести себя противоинтуитивным образом, когда возникает парадокс. Но излишняя профилактическая гигиена здесь излишня — никто еще не заболел! Разумеется, если логический кризис рано или поздно происходит, его следует исследовать, а аргументы прояснить, но и этот процесс может быть проделан интуитивно и неформально. Дух математики как раз и состоит в этом диалоге со своим собственным доказательством.
Дети не только запутываются этим педантизмом — ведь нет ничего более непонятного, чем доказательство очевидного — но даже те, чья интуиция еще пока цела, вынуждены переводить их отличные, прекрасные идеи на этот язык абсурдных иероглифов, который учитель называет «верным». Учитель же льстит себе, полагая, что это каким-то неизвестным образом «оттачивает ум» ученика.
В качестве более серьезного примера, рассмотрим случай треугольника в полукруге.
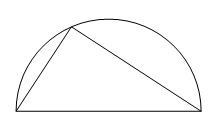
Чудесная закономерность в этом геометрическом узоре состоит в том, что, куда бы вы ни поместили вершину треугольника, угол при этой вершине всегда будет прямым.

В этом случае наша интуиция находится в сомнении. Вовсе даже и не ясно, что это утверждение всегда истинно, даже и не похоже на то — разве не должен угол меняться, когда мы двигаем вершину треугольника по окружности? Это замечательная задача! Всегда ли угол прямой? Если да, почему? Какая чудесная самостоятельная работа! Какая чудесная возможность проявить смекалку и воображение! Разумеется, такой возможности ученикам не дают, и их интерес немедленно сбивается нижеследующим:
ТЕОРЕМА 9.5.
Пусть ∆ABC вписан в полукруг диаметром AC.
Тогда угол ∠ABC прямой.

Доказательство.

Возможно ли что-нибудь более непривлекательное и неэлегантное? Можно ли было сделать доказательство более запутанным и нечитабельным? Это не математика! Доказательство должно быть посланием богов, а не телеграммой Алекса Юстасу! Вот к чему приводит неуемное чувство строгости: к мерзости. Дух доказательства похоронен под грудой путаного формализма.
Математики так не работают. Ни один математик никогда так не работал. Это полное и окончательное непонимание предприятия математики. Математика не занимается возведением барьеров между нами и нашей интуицией, чтобы сделать простое сложным. Математика убирает препятствия нашей интуиции, и сохраняет простое простым.
Сравните эту мешанину со следующим рассуждением одного моего семиклассника: