От чёрных облаков к чёрным дырам - Страница 7

Для преодоления этой трудности астрономы вынуждены были ввести другую шкалу величин, которая более реалистична в том смысле, что учитывает эффект расстояния. Чтобы отличить эту шкалу от шкалы абсолютных величин, новую шкалу называют шкалой видимых звёздных величин. Познакомимся с этой шкалой, прежде чем попытаемся ответить на вопрос: «Какую светимость приписать звезде, имеющей абсолютную звёздную величину, равную 1?»

Связь между абсолютной и видимой звёздными величинами можно понять, обратившись к так называемому «закону обратных квадратов для освещённости». Попробуем понять, в чем смысл этого закона, на примере двух лампочек: яркой (мощностью 1000 Вт) и слабенькой (мощностью 10 Вт).

Пусть мы наблюдаем эти две лампочки с одинакового расстояния. Очевидно, что 1000-ваттная лампочка будет выглядеть значительно более яркой, чем 10-ваттная. Но давайте теперь отодвигать первую лампочку все дальше и дальше от нас. Она станет казаться все менее и менее яркой. На определённом расстоянии её яркость так уменьшится, что она будет казаться такой же слабой, как находящаяся рядом с нами 10-ваттная лампочка. Согласно закону обратных квадратов для освещённости, расстояние, на котором 1000-ваттная лампочка выглядит такой же яркой, как близко расположенная 110-ваттная лампочка, в 10 раз больше, чем расстояние до 10-ваттной лампочки. Таким образом, яркость объекта с точки зрения наблюдателя уменьшается обратно пропорционально квадрату расстояния от светящегося объекта до наблюдателя. Удалив 1000-ваттную лампочку на расстояние, в 10 раз большее расстояния до 10-ваттной лампочки, мы уменьшили видимую яркость лампочки в 10•10=100 раз, так что она, сравнилась с яркостью 10-ваттной лампочки (рис. 10).

Рис. 10. Маленькое пятно на экране, освещённое 10-ваттной лампочкой, так же ярко, как большое пятно, освещённое 1000-ваттной лампочкой, находящейся в 10 раз дальше

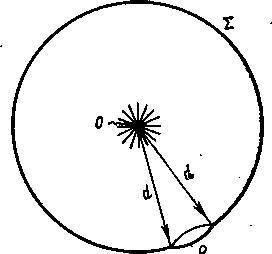
Рис. 11. Свет от источника О равномерно распределяется по поверхности сферы радиусом d. Количество света, падающего на площадку вокруг произвольной точки Р на поверхности Σ, пропорционально площади этой площадки.

Происхождение такого закона можно пояснить с помощью рис. 11. Имеется источник света О, равномерно светящий во всех направлениях. Сферическая поверхность Σ окружает источник О, находящийся в центре этой поверхности. Из школьной геометрии известно, что если радиус поверхности Σ равен d, то площадь поверхности равна 4πd². Как видно из рис. 11, весь свет от источника О равномерно распределяется по всей этой площади. Если L — светимость источника О, то количество энергии, падающей на единицу площади Σ вокруг любой заданной точки Р на поверхности, получается простым делением светимости источника L на полную площадь поверхности Σ:

l = L  . 4πd²

Величина l есть освещённость, измеряемая в точке Р, от источника О. Если точка Р удаляется на большее расстояние, то величина d растёт и l уменьшается обратно пропорционально квадрату d. Именно значение l и определяет видимую яркость источника света.

Представьте теперь, что О — это звезда, а Р — земной наблюдатель. То, что измеряет наблюдатель Р, это не L, а l. Если наблюдатель изучает разные звёзды, он сравнивает не их значения L, а соответствующие значения l. Не зная расстояний до звёзд, наблюдатель имеет в своём распоряжении только значения l, свидетельствующие, насколько одна звезда кажется ярче другой, если смотреть на них из определённого места.

Шкала видимых звёздных величин это такая шкала, в которой звёзды расположены по разрядам в соответствии с их значениями l по той же схеме, что и для шкалы абсолютных звёздных величин в соответствии со значениями L. Так если звезда А кажется наблюдателю в 100 раз ярче звезды В, то видимая звёздная величина В на 5 единиц больше, чем видимая величина А.

Конечно, множитель 100, выбранный выше, особенно прост, так как он соответствует разнице в 5 звёздных величин. Как же связать произвольный множитель с разницей звёздных величин? Ответ даётся с помощью описания разностей, выраженных через отношения ¹. Пусть звезда А имеет светимость L_A, а звезда В — светимость L_B. Тогда абсолютные звёздные величины этих звёзд M_A и M_B отличаются на величину

M_A - M_B = 2.5 lg L_A . L_B

¹ См. приложение, в котором объясняется понятие логарифма

Если отношение M_A/M_B=100, то правая часть приведённого уравнения становится равной 5, как и следовало ожидать. Аналогичное соотношение можно записать для видимых звёздных величин m_a и m_b звёзд А и В, основываясь на значениях их l:

m_A - m_B = 2.5 lg l_A . l_B

Возвратимся теперь к вопросу о том, как приписать какую-то абсолютную величину звезде данной светимости. Прежде всего, нужно установить, чему соответствует нуль на шкале видимых звёздных величин. По соглашению полагают m_A=0, если ² l_A=2,48•10^-8 Вт/м². Тогда приведённое выше соотношение позволяет установить видимую звёздную величину любой звезды, если для неё известна величина l_B. Простой подсчёт приводит к формуле для видимых величин

m_B ≈ -2.5 lg l_B - 19.01,

где l_B измерено в ваттах на квадратный метр.

² Такая шкала величин была предложена в 50-е годы XIX в. Погсоном. В соответствии с такими стандартами, звёзды Альдебаран и Альтаир имеют почти точно первую величину.

Вернёмся теперь к связи между l_B и L_B:

l_B = L_B/4πd_B²,

где d_B равно расстоянию от звезды В до нас. Чтобы сравнивать светимости звёзд, мы должны (теоретически) наблюдать их все с одного расстояния. Опять же по соглашению это расстояние принимается равным 10 парсекам ³¹¹. Значение этой величины как меры расстояния станет яснее в следующей главе, где мы обсудим методы измерений расстояний до звезды. Пока что примем парсек как заданную единицу расстояний.

³¹¹ Парсек (пк) - единица расстояний в астрономии. 1 пк = 3,26 светового года = 206265 астрономических единиц = 3,08 • 10¹⁶м - Прим. ред.

Тогда правило гласит, что абсолютная звёздная величина M_B звезды В равна видимой звёздной величине этой звезды, которую она бы имела, если бы находилась от нас на расстоянии 10 пк. Иными словами, положим в предыдущей формуле d_B = 10 пк, вычислим соответствующее значение l_B, а затем переведём в значение m_B по формуле для видимых звёздных величин. Ответ, который мы получим, равен M_B. Естественно, чтобы вычислить M_B для звезды В, нужно знать её видимую звёздную величину и истинное расстояние до звезды от нас. Задав эти величины, с помощью описанной процедуры получим

M_B = m_B - 5 lg d_B + 5 .