Нестандартные задачи по математике в 4 классе - Страница 2

Задача 6. В двух кучах лежат камни. Двое играющих по очереди берут из любой кучи произвольное число камней. Выигрывает тот, кто возьмет последний камень. Тебе разрешается начать игру или предоставить партнеру право первого хода. Как ты будешь играть?

Суть игры в том, чтобы уравнивать число камней в кучах. Если один игрок уравняет их, то другой обязательно нарушит это равенство, и т. д. Число камней все время убывает, и когда-нибудь игрок, уравнивающий число камней в кучах, доведет это равенство до 0–0, то есть выиграет.

Отметим, что очень желательно организовать эту игру. Камни для этого иметь необязательно. Можно просто написать на доске:

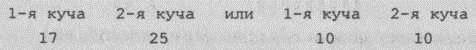
В первом случае надо начинать первым, забирая из второй кучи 8 камней (уравнивая кучи). Во втором случае надо предоставить первый ход противнику и каждым своим ходом уравнивать кучи.

Ответ: Если число камней в кучах одинаково, нужно предоставить первый ход партнеру, а если неодинаково, — начать игру, уравнивая число камней в кучах.

Задача 7. Шифром Юлия Цезаря по правилу «прибавь четыре» зашифруй фразу «век живи — век учись».

Как мы писали в аналогичной книге для третьеклассников, шифр Юлия Цезаря состоит в следующем. Алфавит пишется по кругу (за буквой я следует буква а), и каждая буква шифруемой фразы заменяется другой, следующей за ней (или перед ней) на определенное число букв. Шифр «прибавь четыре» означает, что каждую букву фразы «век живи — век учись» нужно заменять четвертой от нее буквой:

Ответ: Ёио кмём — ёио чымха.

Задача 8. Известно, что а + b = 7. Чему равно (а + 8) + b? Задачу можно изложить, например, так. У Вовы в двух карманах было 7 рублей. Он положил в левый карман еще 8 рублей. Сколько теперь у него денег в обоих карманах?

Ответ: 15.

Задача 9. Переложи одну спичку, чтобы равенство:

стало верным (это можно сделать двумя способами).

Надо воспользоваться тем, что в римской нумерации XI — это 11, а IX — это 9.

Ответ:

Задача 10. Друзья при прощании обменялись фотографиями. Фотографий понадобилось 20. Сколько было друзей?

Решение осуществим подбором. Если бы друзей было двое, то фотографий понадобилось бы всего две. Если бы их было трое, то понадобилось бы шесть фотографий, как это видно из рисунка:

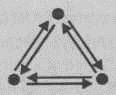
Если друзей четверо, то из следующего рисунка видно, что фотографий нужно 12:

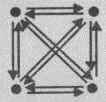
А если друзей пятеро, то фотографий нужно 20:

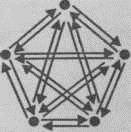
Можно рассуждать и более квалифицированно: каждый должен подарить на одну фотографию меньше, чем всего имеется друзей. Произведение двух последовательных чисел равно 20, если большее из чисел равно 5.

Ответ: 5.

Задача 11. У Кати вдвое больше пятерок, чем у Вовы, а у него на 6 пятерок меньше, чем у Кати. Сколько пятерок у Вовы?

Эту задачу можно решить арифметически, а можно с помощью уравнения. Если в классе есть дети, которые могут сразу решить эту задачу, нужно попросить их придумать, как объяснить решение остальным. Это относится и к арифметическому, и к алгебраическому решению.

Арифметическое решение подсказывается рисунком:

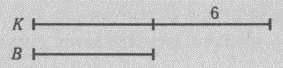
Сразу видно, что у Вовы 6 пятерок, а у Кати их 12.

Может показаться, что если задача решается так просто, то это значит, что не нужно ее решать другим способом. Однако, именно на легких задачах можно научиться новому методу решения. Данная задача очень для этого удобна. Мы вызываем к доске ученика и просим начать записывать уравнение. Что можно записать? Конечно, знак равенства:

=

Этим самым начат поиск следующих шагов: что чему равно в данной задаче? Может быть, что-то равно 6? Дописываем:

= 6.

Многие догадаются, что шести равна разность числа Катиных и числа Вовиных пятерок. И мы так и запишем:

(число Катиных пятерок) — (число Вовиных пятерок) = 6.

Получилось уравнение. Но в нем слишком много неизвестных — два. Хорошо бы выразить их через одно неизвестное х. Кстати, вспоминаем, что спрашивается в задаче. И приходим к мысли обозначить через х именно эту величину — число Вовиных пятерок. Тогда:

(число Катиных пятерок) — х = 6.

Теперь уже многие догадаются, что число Катиных пятерок равно 2 х, и уравнение примет вид:

2х — х = 6.

Ответ: 6.

Задача 12. Эту фигуру:

нужно обвести карандашом, не отрывая его от бумаги и не проводя никакую линию дважды.

Решение очевидно. Начинать обводку можно с любой точки.

Задача 13. Известно, что а + b = 12. Чему равно а + (b + 5)?

Надо попросить детей придумать текст задачи на эту тему (см., например, задачу 8).

Ответ: 17.

Задача 14. У Саши втрое больше марок с портретами русских писателей, чем у Пети, а у Пети на 4 таких марки меньше, чем у Саши. Сколько таких марок у Пети?

Арифметическое решение подсказывается рисунком:

Сразу видно, что у Саши 6 таких марок, а у Пети их 2.

Алгебраическое решение начинаем с записи знака равенства:

=

Но что чему равно в данной задаче? Может быть, что-то равно 4? Дописываем:

= 4.

Многие догадаются, что четырем равна разность числа Сашиных и числа Петиных марок:

(число Сашиных марок) — (число Петиных марок) = 4.

Получилось уравнение с двумя неизвестными. Выразим эти неизвестные через один и тот же х. Обозначим через х ту величину, о которой спрашивается в задаче: х — число Петиных марок. Получается, что

(число Сашиных марок) — х = 4.

Теперь уже многие догадаются, что число Сашиных марок равно Зх, и уравнение примет вид:

3х — х = 6.

Ответ: 3.

Задача 15. Эту фигуру:

нужно обвести карандашом, не отрывая его от бумаги и не проводя никакую линию дважды.

Решение очевидно. Начинать обводку можно с любой точки.

Задача 16. Из надписи 1234567891011121314151617181920 вычеркни 21 цифру, не меняя порядка цифр, чтобы оставшееся число было а) возможно большим; б) возможно маленьким.

Всего в надписи 31 цифра. Нужно оставить из них 31 — 21 = 10 цифр.

а) Чтобы число было наибольшим, нужно сделать его старшие цифры наибольшими. Первой сделаем цифру 9, вычеркнув первые восемь цифр: 91011121314151617181920. Сделать второй цифрой 9 нам не удастся, так как тогда останется такое число: 9920, а нам нужно число десятизначное. Не удастся сделать второй цифрой и 8, и 7, а вот 6 можно сделать второй цифрой, вычеркнув 13 цифр. Остальные цифры останутся невычеркнутыми.