Научная обективность и ее контексты - Страница 38

Чтобы избежать какого бы то ни было проникновения в наш дискурс эпистемологического дуализма и не создавать впечатления, что теоретические термины играют здесь некоторого рода метатеоретическую роль по отношению к операциональным терминам (поскольку мы сказали, что они используются также, чтобы «говорить об» объектах, образованных операциональными атрибутами), возьмем пример из повседневной жизни. Предположим, что для опознания одного человека из некоторой группы мне нужны три или четыре эмпирические свойства, такие как цвет его глаз и волос, его рост, форма носа или рта и т. п. Коль скоро я опознал его, мне уже не нужно больше говорить о нем только с помощью этих нескольких предикатов. Я, очевидно, могу приписать ему (т. е. высказать о нем) несколько дополнительных признаков, причем некоторые из них могут быть эмпирическими (как цвет кожи, или тот факт, что он смеется), а другие – неэмпирическими (например, что он доктор, или человек религиозный, или имеет определенный возраст).

Ясно, что исходные «базовые» предикаты были эмпирическими, и мы нуждались в них, чтобы зафиксировать референт нашего обсуждения. Это значит, что, например, если мы скажем, что м-р Х. доктор, мы можем утверждать, что мы высказываем это свойство о человеке, которого имеем в виду, только если этот м-р Х. есть в то же время то лицо в нашей группе, которое идентифицируется нашими базовыми предикатами. Но м-ру Х. могут приписываться разного рода свойства, как эмпирические, так и неэмпирические, и мы можем использовать любые из них, говоря о человеке, которого имеем в виду, если существует сеть предложений, которая, в случае надобности, сможет показать, как соотнести то, что мы говорим, с базовыми предикатами, которые мы выбрали для его идентификации. В этом смысле мы можем также сказать, что мы расширили описание нашего «объекта», поскольку все используемые нами новые предикаты на самом деле улучшают его определение, привнося новые элементы в логическую сеть, выражающую структуру теории, ограничивая тем самым область того, что может быть объектом именно этого сорта[136].

Вернемся теперь к рассматриваемому вопросу. Мы можем утверждать, что базовые предикаты «определяют» научный объект, не потому, что они имеют внутренне привилегированную природу, а просто потому, что им в явном виде была поставлена задача идентифицировать его. Но после этого в дискурс может войти еще много других предикатов, если только мы в случае надобности можем показать, что они связаны с базовыми. В любой теории, предлагаемой в некоторой эмпирической науке, некоторый логический путь должен вести от любого предложения, содержащего только предикаты, отличные от базовых (например, от предложения, содержащего только теоретические термины), по крайней мере к одному предложению, содержащему только базовые предикаты. Это убеждает нас в том, что мы все еще говорим о предполагаемых нами объектах. Кроме того, в этом причина, по которой проверяемость, как мы уже подчеркивали, является таким фундаментальным требованием для всех эмпирических теорий. Собственно говоря, без проверяемости мы никогда не могли бы быть уверены, что теоретические положения теории касаются ее объектов[137].

В предшествующем дискурсе одно предположение кажется слишком легко принятым, а именно, что можно провести четкое различие между операциональными и теоретическими (или неоперациональными) предикатами, поскольку один из самых респектабельных тезисов новейшей философии науки состоит в том, что это различие не существует между наблюдательными и теоретическими терминами (а похоже, что наши операциональные термины можно приравнять к наблюдательным терминам, о которых здесь идет речь)[138]. Этот вопрос будет рассмотрен позже. Пока что примем, что имеет смысл различать (резко или иначе) операциональные понятия (которые мы для краткости будем называть О-понятиями) и теоретические понятия (которые будем называть Т-понятиями). А сейчас мы хотим рассмотреть случай термина «P», родового предиката, связанного с другими предикатами в рамках некоторой теории, и сравнить его с аналогичным термином «P'».

Прежде всего мы видим, что значением P является, по крайней мере отчасти, логическая сеть, связывающая его со всеми остальными терминами теории, так что это значение одновременно определяется присутствием определенных О-терминов и Т-терминов в этой сети и конкретными связями между этими терминами (или, если кто-нибудь это предпочитает, структурой сети). Рассмотрим теперь случай, когда P и P' связаны с одними и теми же О-терминами и Т-терминами посредством различных связей, и случай, когда P и P' связаны посредством одной и той же логической сети с по крайней мере отчасти разными О-терминами и Т-терминами. Будет ясно, что в этих случаях значение P и P' не может быть одним и тем же. Такого рода ситуацию можно схематически представить следующими четырьмя фигурами.

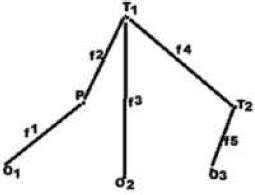
Рис. 1

Рис. 2

Случай А (рис. 1 и 2). Мы принимаем, что понятия остаются теми же самыми (O1, O2, O3, T1, T2), но логические отношения меняются (f3, f4, f5 исчезают, а новые функции g1, g2, g3 связывают P непосредственно с O2, O3, T2).

Рис. 3

Рис. 4

Случай В (рис. 3 и 4). Мы принимаем, что понятия и функции остаются теми же самыми, но образуют отчасти другие конфигурации.

В обоих случаях значение P и P' не может быть одним и тем же. Нетрудно построить и другие подобные ситуации.

В вышеприведенных диаграммах линии между точками указывают на определенные логические отношения между соответствующими предикатами (которые мы можем представлять себе как представленные уравнениями или функциями, содержащими предикаты), и мы видим, что даже если о предикатах можно сказать, что они остаются теми же самыми, изменения логических корреляций, происходящие при переходе от рис. 1 к рис. 2 или от рис. 3 к рис. 4, изменят значение Р и сделают его отличным от значения P' (но и другие значения тоже изменятся, хотя мы и не меняли других терминов). С другой стороны очевидно, что если структура сохранена, но хотя бы один из предикатов изменился, это изменит значение P' (как и остальных понятий).

Тот факт, что значение понятия контекстно-зависимо, можно выразить, сказав, что оно зависит от значений других понятий и от его логических связей с ними, откуда также следует, что это в свою очередь влияет на значения всех понятий, с которыми оно связано.

Такая зависимость осознана не так уж давно. Можно считать, что она официально вошла в современную методологию науки через новый подход к аксиоматическому методу, когда он стал рассматриваться не просто как средство наведения дедуктивного порядка в некоторой дисциплине, а как нечто способное создавать, по крайней мере в некоторой степени, сами объекты этой дисциплины. Разница между этими двумя позициями довольно очевидна. Если рассматривать аксиоматизацию как способ дедуктивного упорядочения некоторой дисциплины, то приходится рассматривать по крайней мере какое-то количество терминов, входящих в аксиомы, как имена тех единиц, которые эта дисциплина предполагает описывать, а «значения» этих терминов могут рассматриваться как их отнесенность к данным объектам. Но если рассматривать аксиоматизацию как нечто такое, что должно «создать» некоторую дисциплину, никакие объекты не предполагаются существующими, а аксиомы должны некоторым образом быть способны иметь значение, не имея, строго говоря, референтов. Если это так, значение терминов должно по необходимости возникать из взаимосвязей разных понятий друг с другом, и если возникает вопрос о референтах, он может касаться только возможности обнаружить некоторую структуру из объектов, отношения между которыми можно было бы поставить в соответствие со связями понятий, выраженными в аксиомах, так чтобы они их верно представляли. Такая аксиоматизация в явном виде была предложена Гильбертом в его «Основаниях геометрии» 1889 г. Эта книга отличалась от традиционных учебников геометрии того времени не тем, что она защищала новую геометрию (на самом деле ее содержание все еще сравнимо с содержанием обычной геометрии), но тем, что в ней по-другому понимался аксиоматический метод. «Точка», «прямая линия», «плоскость» и т. д. представлялись уже не как имена специфических геометрических единиц, а как термины, значения которых могли «контекстуально» определяться всеми аксиомами и которые в силу этого могли иметь в качестве референтов любые объекты, способные удовлетворять этим аксиомам[139].