Наша математическая вселенная. В поисках фундаментальной природы реальности - Страница 4
Космические вопросы
Мальчик поднимает руку, и я жестом предлагаю задать вопрос. «А космос тянется без конца?» – спрашивает он.
Вот это да! Я только что закончил небольшой рассказ об астрономии в «Детском уголке» в Уинчестере (Массачусетс, США), где мои дети проводят время после уроков, и вся очаровательная группа детсадовцев, сидя на полу, глядит на меня большими вопрошающими глазами, ожидая ответа. А этот пятилетний малыш только что задал вопрос, на который я не могу ответить! На самом деле, ответить на него не может никто на планете. И все же это не безнадежный метафизический вопрос, а серьезный, научный: теории, о которых я вам расскажу, дают на этот счет ясные предсказания, а уже идущие эксперименты могут пролить на него еще больше света. Я считаю, что это важнейший вопрос о фундаментальной природе физической реальности, и он приведет нас к двум типам параллельных вселенных (гл. 5).
Год за годом следя за мировыми новостями, я чувствовал, как во мне растет мизантропия, но всего за несколько секунд этот малыш укрепил мою веру в потенциал человечества. Если пятилетний ребенок может говорить такие вещи, представьте только, на какие достижения способны взрослые в подходящих обстоятельствах! Он также напомнил мне о важности обучения. Все мы от рождения наделены способностью удивляться, но в какой-то момент школа обычно умудряется вытравить ее из нас. Я чувствую, что важнейшая моя задача как учителя не изложить факты, а разжечь эту угасшую страсть к вопрошанию.
Я люблю вопросы. Особенно глобальные. Я чувствую себя счастливым, потому что могу тратить львиную долю своего времени на интересные вопросы. То, что я могу называть эту деятельность работой и зарабатывать так на жизнь, – большая удача, превосходящая мои самые смелые надежды. Вот список из шестнадцати вопросов, которые мне чаще всего задают:
1. Как может пространство не быть бесконечным?
2. Как бесконечное пространство может быть создано за конечное время?
3. Куда расширяется Вселенная?
4. Где именно в пространстве произошел наш Большой взрыв?
5. Произошел ли наш Большой взрыв в одной точке?
6. Если возраст нашей Вселенной всего 14 млрд лет, то как мы видим объекты на расстоянии 30 млрд световых лет?
7. Не нарушают ли галактики, удаляющиеся быстрее света, теорию относительности?
8. Галактики действительно удаляются от нас – или это пространство расширяется?
9. Расширяется ли Млечный Путь?
10. Найдены ли следы сингулярности Большого взрыва?
11. Не нарушает ли закон сохранения энергии возникновение материи почти из ничего в ходе инфляции?
12. Что стало причиной нашего Большого взрыва?
13. Что было до нашего Большого взрыва?
14. Какова окончательная судьба нашей Вселенной?
15. Что такое темная материя и темная энергия?
16. Действительно ли мы несущественны для Вселенной?
На одиннадцать вопросов мы ответим в следующих четырех главах. Но сначала вернемся к детсадовскому вопросу, центральному для всей первой части книги: тянется ли космос бесконечно?
Насколько огромен космос?
Однажды отец дал мне совет: «Если ты задумался над сложным вопросом, на который не можешь ответить, займись сначала более простым вопросом, на который не можешь ответить». Последуем этому совету и выясним, какой минимальный размер должно иметь пространство, чтобы не противоречить наблюдениям. На рис. 2.1 показано, как поразительно выросли эти размеры: сегодня мы знаем, что пространство по крайней мере в миллиард триллионов (1021) раз превышает наибольшие расстояния, знакомые древним охотникам и собирателям, – те, что они могли пройти за время своей жизни.
Более того, на рисунке видно, что расширение наших горизонтов было не уникальным событием, а повторялось многократно. Всякий раз, когда людям удавалось заглянуть дальше и построить карту более крупных структур Вселенной, мы обнаруживали, что все известное нам прежде является частью чего-то большего. Как показано на рис. 2.2, наша родина – это часть планеты, которая является частью Солнечной системы, которая является частью Галактики, которая является частью паттерна скоплений галактик, который является частью наблюдаемой Вселенной, которая является частью одного или более уровней параллельных вселенных.

Рис. 2.1. Нижнее ограничение на размер нашей Вселенной постоянно растет. Заметьте, что шкала на вертикальной оси очень крутая: с каждым делением размеры возрастают в 10 раз.
Люди думали, что все видимое – это и есть все существующее, и высокомерно помещали себя в центр мироздания. Таким образом, недооценка была лейтмотивом наших поисков понимания космоса. И все же рис. 2.1 отражает и другую мысль, вдохновляющую меня: мы многократно недооценивали не только размеры космоса, но и силу человеческого разума, способного его понять. У наших пещерных предков был такой же большой мозг, как и у нас, и поскольку они не тратили вечера на просмотр телевизора, я уверен, что они задавались вопросами вроде: «Что это там такое в небе?» или «Откуда это все взялось?» Они пересказывали друг другу красивые мифы и легенды, но им и в голову не приходило, что они способны найти настоящие ответы на эти вопросы. И что секрет заключается не в освоении полетов в космос для изучения небесных тел, а в том, чтобы позволить взлететь разуму.
Нет лучшей гарантии неудачи, чем признать, что успех невозможен, а значит, не надо и пытаться. Задним числом кажется, что многие великие прорывы в физике могли случиться раньше, поскольку необходимые инструменты уже существовали. Проведем аналогию с хоккеем: люди не забивали шайбу в пустые ворота просто потому, что считали свою клюшку сломанной. В следующих главах я поделюсь впечатляющими примерами того, как Исаак Ньютон, Александр Фридман, Георгий Гамов и Хью Эверетт преодолели эту неуверенность. Мне очень нравится высказывание нобелевского лауреата Стивена Вайнберга: «Так часто бывает в физике – ошибка не в том, что мы слишком серьезно относимся к своим теориям, а в том, что не воспринимаем их достаточно серьезно».
Сначала выясним, как определить размеры Земли и расстояние до Луны, Солнца, звезд и галактик. На мой взгляд, это одна из самых ярких детективных историй всех времен, которая, можно сказать, породила современную науку. Так что я горю желанием поделиться ею с вами, как закуской перед основным блюдом – последними достижениями космологии. Как вы увидите, первые четыре вопроса не требуют ничего сложнее измерений углов. Они также проиллюстрируют, насколько важно удивляться, казалось бы, банальным наблюдениям – ведь они могут оказаться ключевыми уликами.
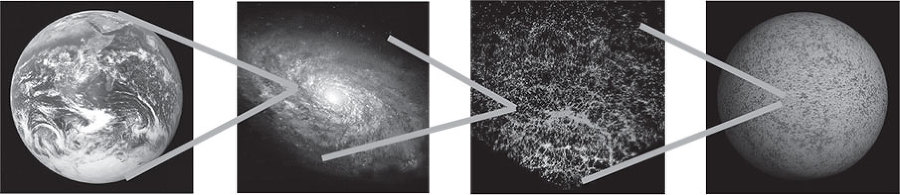
Рис. 2.2. Наша родина – это часть планеты (слева), которая является частью Солнечной системы, которая является частью Галактики (посередине слева), которая является частью паттерна скоплений галактик (посередине справа), которая является частью наблюдаемой Вселенной (справа), которая может быть частью одного или более уровней параллельных вселенных.
Размеры Земли
С древности люди замечали, что у корабля, уходящего за горизонт, корпус исчезает из виду раньше парусов. Это наводило на мысль, что поверхность океана искривлена и что Земля имеет сферическую форму, подобно Солнцу и Луне. Древние греки обнаружили прямое тому подтверждение, заметив, что Земля во время лунного затмения отбрасывает на Луну круглую тень (рис. 2.3). Хотя размеры Земли нетрудно оценить по виду парусных судов[5], Эратосфен около 2,2 тыс. лет назад выполнил более точные измерения, догадавшись, как воспользоваться для этого измерением углов. Он знал, что в египетской Сиене в день летнего солнцестояния Солнце в полдень оказывалось прямо над головой, однако в Александрии, расположенной на 794 км севернее, оно в это время находилось на 7,2° южнее зенита. Отсюда ученый вывел, что перемещение на 794 км соответствует прохождению 7,2° из 360° окружности Земли, а значит, длина этой окружности составляет около 794 км × 360° / 7,2° ≈ 39,7 тыс. км, что удивительно близко к современному значению (40 тыс. км).