Наибольший общий делитель (НОД) - Страница 1
- 1
Предисловие
В данной книге приводятся четыре алгоритма нахождения наибольшего общего делителя, необходимая теория, формулы, 29 примеров с решениями, 140 упражнений с ответами.
Наибольший общий делитель (НОД) [двух чисел]
Теоретический материал
В таблице приведем два способа определения НОД.

Алгоритм №0.
Не является рациональным способом нахождения наибольшего общего делителя двух чисел
Выпишем все делители чисел 32 и 24.
Делители числа 32: 1, 2, 4, 8, 16, 32.
Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.
Общими делителями 24 и 32 являются: 1, 2, 4, 8.
Наибольший из них – 8. Обозначается НОД(24;32)=8.
Замечание. Вышеизложенный алгоритм №0 не является рациональным способом нахождения НОД (им можно воспользоваться в том случае если вы забыли способы нахождения НОД).
Определение 3. Натуральные числа a и b называют взаимно простыми, если их наибольший общий делитель равен 1, то есть НОД(a; b) = 1.
Иначе выражаясь, если числа a и b не имеют никаких общих делителей, кроме 1, то они взаимно просты.
Пример 3.
1) Числа 2 и 5 взаимно простые (и сами они простые);
2) 2 и 9 взаимно простые (2 – простое, 9 – составное);
3) 8 и 9 взаимно простые (и оба они составные);
Замечание. Как видно из случаев, приведенных в примере 2, понятия «простые числа» и «взаимно простые числа» не имеют особой связи между собой.
Правило. Если одно из данных чисел [36] является делителем другого числа [72], то оно [36] будет являться наибольшим общим делителем данных чисел [72 и 36].
Формулы, необходимые для алгоритма №1
Для вычисления по алгоритму №1 необходимо знать формулы


Замечание. Формулу a0=1 мы будем использовать «справа налево», то есть 1=a0.
Единицу мы будем представлять как 20, как 30, как 50, как 70, как 110, …
1=20, 1=30, 1=50, 1=70, 1=110, …
Алгоритм №1
Рекомендуемый способ нахождения
наибольшего общего делителя двух чисел
Алгоритм №1.
1) Разложить данные числа на простые множители;
2) выбрать наименьшие степени множителей из разложений данных чисел;
3) перемножить выбранные множители в наименьших степенях.
Кратко (для заучивания, нестрогое правило): разложить на множители, выбрать наименьшие степени, перемножить.

Пример 1. Найти НОД (18; 14).
1) Разложим на простые множители числа 18 и 14:

18=2×32=2×32×1= 21×32×70,
14=2×7=21×1×71=21×30×71.
2) В обоих разложениях множитель 2 встречается в первой степени. Значит, выписываем множитель 21 (НАИМЕНЬШИЙ!!!).
Множитель 3 встречается во второй и нулевой степени, значит, выписываем 30 (наименьший).
Множитель 7 встречается в первой и нулевой степени, значит, выписываем 70 (наименьший).
3) 21×30×70=2×1×1=2.
Ответ: НОД(18; 14)=2.
Замечание. Нулевая степень в разложении числа обозначает, что данный множитель входит в разложение числа ноль раз. Запись 18=21×32×70 означает, что множитель 7 входит ноль раз в разложение числа 18.
Пример 2. Найти НОД (36; 30).
1) Разложим на простые множители числа 36 и 30:

36=22×32= 22×32×1= 22×32×50,
30=2×3×5=21×31×51.
2) Множитель 2 встречается во второй и первой степени, значит, выписываем 21 (наименьший).
Множитель 3 встречается во второй и первой степени, значит, выписываем 31 (наименьший).
Множитель 5 встречается в первой и нулевой степени, значит, выписываем 50.
3) 21×31×50=2×3×1=6
Ответ: НОД(36; 30)=6.
Пример 3. Найти НОД (9; 10).
1) Разложим на простые множители числа 9 и 10:

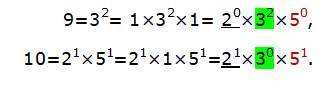
2) Множитель 2 встречается в первой и нулевой степени. Значит, выписываем множитель 20.
Множитель 3 встречается во второй и нулевой степени, значит, выписываем 30. Множитель 5 встречается в первой и нулевой степени, значит, выписываем 50.
3) 20×30×50=1×1×1=1.
Ответ: НОД(9; 10)=1.
Пример 4. Найти НОД (48; 88).
1) Разложим на простые множители числа 48 и 88:

48=24×31= 24×31×110,
88=23×30×111.
2) Множитель 2 встречается в третьей и четвертой степени. Значит, выписываем множитель 23.
Множитель 3 встречается в первой и нулевой степени, значит, выписываем 30
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.