Мир математики. т 40. Математическая планета. Путешествие вокруг света - Страница 26
Пример рефлексивного, симметричного и транзитивного отношения — отношение «быть одного возраста с». Оно очевидно обладает рефлексивностью, так как любой человек будет одного возраста с самим собой. Оно симметрично, так как если А одного возраста с В, то В одного возраста с А. Оно также транзитивно: если А одного возраста с В, а В одного возраста с С, то А и С одного возраста.
Большинство отношений, обладающих рефлексивностью, симметричностью и транзитивностью, являются отношениями эквивалентности, поэтому совокупности субъектов или элементов, связанных такими отношениями, называются классами эквивалентности.
Классы эквивалентности — это то, с чем каждый день имеют дело все люди (хотя при этом они используют не термины, а обычные слова). Когда мы говорим «яблоко», то имеем в виду вид фруктов, но говорим о нем как о классе эквивалентности на множестве всех фруктов. Если мы говорим «ранетка», то имеем в виду класс эквивалентности на множестве яблок. «Является яблоком» и «является ранеткой» — отношения эквивалентности на множестве фруктов и яблок соответственно.
Существуют ли отношения эквивалентности среди родственных связей? В следующей таблице приведены свойства, которыми обладают отношения кровного родства и свойства (выделены серым цветом). Пол людей в таблице не учитывается, то есть отношения «является братом» и «является сестрой» равнозначны.
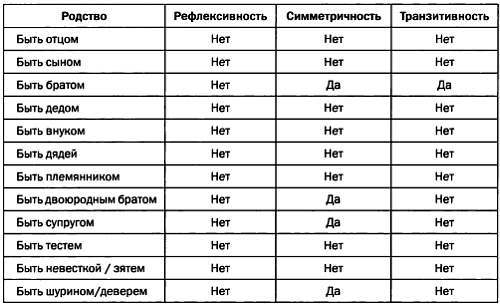
Так как никакое из этих отношений не обладает всеми тремя свойствами, то ни одно из них не является отношением эквивалентности. Ближайший кандидат — отношение «быть братом»: оно симметрично и транзитивно, но не обладает рефлексивностью.
В нашей культуре геометрической моделью структуры родства является генеалогическое дерево. На нем изображены отношения кровного родства и брака. На следующем дереве браки обозначены горизонтальными линиями.
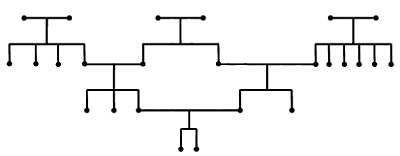
Отношения между дедами, отцами, сыновьями и внуками, связывающие разные поколения, составляют вертикальную ось системы. Отношения кровного родства на уровне каждого поколения, то есть отношения, обозначенные на схеме горизонтальными линиями, — это связи между родными и двоюродными братьями и сестрами. Отношения свойства — это связи между супругами и их родственниками.
Совокупность отношений кровного родства и свойства определяет другие отношения, которые на генеалогическом древе обозначены диагоналями. Это родственные связи между дядьями и племянниками, тестями, тещами, невестками и зятьями.
Если говорить о поле, наша система обладает двойственностью в том смысле, что в несимметричных отношениях (таких большинство) присутствуют дополняющие элементы. В отношениях между родными и двоюродными братьями и сестрами, между супругами и их родственниками дополняющие элементы необязательны. Если А — родной или двоюродный брат, супруг или родственник супруга В, то В — родной или двоюродный брат, супруг или родственник супруга А. Но в асимметричных отношениях дело обстоит иначе:
дед — внук
отец — сын
тесть — зять
дядя — племянник.
Генеалогическое древо — геометрическая модель отношений родства в том виде, в каком они понимаются в нашей культуре. Теперь составим алгебраическую модель отношений кровного родства (за исключением родных и двоюродных братьев, дядей и племянников), охватывающую пять поколений (деды, отцы, наше поколение, дети и внуки). Представители различных поколений обозначены числами: 0 обозначает поколение, к которому принадлежит читатель, отрицательные числа — предшествующие поколения (-1 — отцы, — 2 — деды), положительные числа — последующие поколения (1 — дети; 2 — внуки).
Будем предполагать, что читатель принадлежит к поколению 0. Тогда операция (—1) * (1) означает «дед моего внука», то есть я, то есть 0. Проведя аналогичные рассуждения, заполним таблицу.
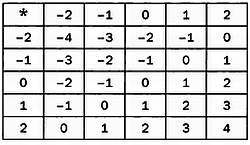
Операция *, определенная в этой таблице, эквивалентна сумме цифр в соответствующем столбце и строке. Композиция отношения с самим собой обозначается символом (°) и может представлять собой исходное либо какое-то другое отношение.
Отец ° отец = дед.
Сын ° сын = внук.
Брат ° брат = брат.
Варлпири — аборигены, живущие в Австралии. Сложная структура их родственных отношений определяет модели поведения, взаимоотношений, общественной и политической организации, а также проведение ритуалов. Для варлпири, как и для других народов, все сущее связано между собой в единой картине мира, определенной мифологическими предками, которые сотворили горы и реки, флору и фауну и дали всему названия. Предки варлпири также указали, что является священным и какие ритуалы и церемонии следует проводить.
Структура родственных отношений варлпири описывается рядом правил. Каждый абориген принадлежит к одной из восьми групп. Так, группа, к которой принадлежат дети от брака, отличается от групп, к которым принадлежат родители, и определяется по материнской линии. Если мы обозначим группы числами от 1 до 8, то дочь женщины из группы 4 будет принадлежать группе 2, ее дочь — группе 3, дочь последней — группе 1. Аналогично определяются взаимосвязи между группами 5, 6, 7 и 8. Следовательно, по материнской линии существует два непересекающихся цикла четвертого порядка, {1, 4, 2, 3} и {3, 7, 6, 8}.
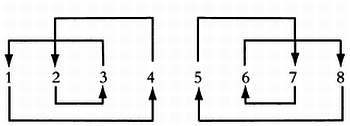
Циклы, определяемые по материнской линии в структуре родственных отношений австралийских аборигенов варлпири.
Еще одно правило заключается в том, что браки не могут заключаться в пределах одной группы. В следующей геометрической модели структуры родства браки обозначены пунктирными линиями.
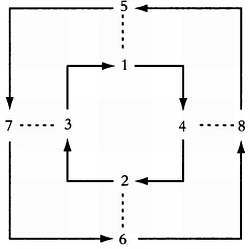
Браки в структуре родственных отношений варлпири.
Так как группы, к которым принадлежат мужчины, определяются на основе женских, то если мужчина из группы 1 женится на женщине из группы 5, их сын будет принадлежать к группе 7. Следовательно, он женится на женщине из группы 3, а сын от их брака вновь будет принадлежать к исходной группе 1. По отцовской линии определено четыре цикла второго порядка: {1, 7}, {2, 8}, {3, 6} и {4, 3}.
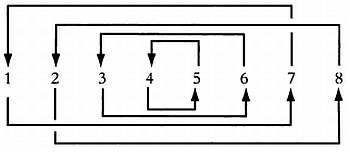
Циклы, определяемые по отцовской линии в структуре родственных отношений варлпири.
Таким образом, имеем два цикла четвертого порядка по материнской линии и четыре цикла второго порядка по отцовской линии, которые в сумме охватывают все восемь групп структуры родственных отношений. Упомянутые восемь групп могут объединяться разными способами и образовывать множества, для которых определяются различные аспекты жизни в обществе. К примеру, группы, описывающие права наследования, отличаются от групп, описывающих допустимые браки или объединения для проведения каких-либо работ.
Формальное математическое описание этой структуры есть не что иное, как практическое применение понятия, которое в теории групп называется группой изометрии восьмого порядка. Чтобы проиллюстрировать эту идею, покажем, как изометрии квадрата образуют группу изометрии восьмого порядка.