Мир математики. т 40. Математическая планета. Путешествие вокруг света - Страница 23
Этот колам образован тремя кривыми. Две из них одинаковы: одна получается из другой поворотом на 90°. Обе эти кривые симметричны относительно поворота на 180°. Третья кривая образует фигуру, симметричную относительно поворота на 90°. Она построена на двойной сетке из 25 точек, которые расположены в виде двух квадратов размерами 3 х 3 и 4 х 4, причем первый находится внутри второго.


Колам.
Традиция изображать колам на юге Индии насчитывает несколько веков, и ее истоки, возможно, лежат в культурах Центральной Африки. В этих узорах математическая мысль состоит не столько в симметричности итоговых фигур, сколько в четких методах построения. Именно женщины являются хранителями многовековой традиции и математических знаний, которые ежедневно используются в домашнем хозяйстве. Методы изображения колам передаются от матери к дочери, совершенствуются и достигают таких высот, что ими восхищаются математики всего мира.
В одиннадцатой главе трактата «Дао дэ цзин» отмечается, что полезность колес, сосудов и окон проистекает из их пустоты. В самом деле, люди с доисторических времен стремятся отделить небольшие участки бесконечного пространства, которое нас окружает, создавая границы: для колеса нужна окружность, для сосуда — сферическая поверхность, для окна — плоская стена с отверстием в нем.
В разные годы были созданы самые разные плоские и криволинейные поверхности из бесконечного множества материалов и бесконечным множеством способов. Чаще всего для создания поверхностей и объемных тел применялось плетение волокон растений — этим методом создаются как плоские поверхности — циновки рогожи, стены и крыши домов, так и объемные фигуры — корзины, клетки, загоны для птицы и мячи для игры в сепактакрау (разновидность волейбола в Юго-Восточной Азии, но игра происходит не руками, а ногами).
Творческие способности и умения мастеров со всего света заслуживают восхищения как с художественной точки зрения, так и с точки зрения технологий. Паулус Жердес, исследователь этноматематики из Мозамбика, изучил узоры и формы, применяемые мастерами плетения из лозы. Среди геометрических задач, связанных с лозоплетением, выделяется следующая: каким должен быть угол сгиба, если нужно обернуть один прут вокруг другого прута такой же толщины? Ответ — 60° — определяется при помощи тригонометрических расчетов. На практике этот угол определяется складыванием лозы вдвое, как показано на рисунке.

Богатство орнаментов в лозоплетении.
Мячи для игры в сепактакрау во всей Юго-Восточной Азии изготавливаются из ротанга, который также используется для изготовления мебели. Ротанг напоминает ивовый прут, но в сечении эти стебли ротанговой пальмы не округлые, а плоские. Ротанг гибкий, но очень прочный, и сломать его нелегко даже при ударах ногами, как во время игры в сепактакрау.

Мастер демонстрирует мяч для игры в сепактакрау.
Мастера, изготавливающие плетеные мячи, не используют никаких схем и не проводят никаких вычислений, но наблюдая за ними во время работы, сложно поверить, что почти идеальную сферу можно изготовить без помощи математики.
Впрочем, математика все же используется, хоть и не в явной форме.
В математике сфера определяется как множество точек, расположенных на одинаковом расстоянии от точки, называемой центром. Однако при изготовлении мячей для игры в сепактакрау это определение бесполезно. Суть метода плетения идеальных мячей (если пренебречь неизбежными погрешностями и неровностями самого ротанга) заключается не в определении центра и радиуса сферы, а построении многогранника постоянной кривизны. Мастер начинает работу с того, что сплетает пять стеблей ротанга в форме как можно более правильного пятиугольника. Затем мастер выбирает несколько вершин пятиугольника и продевает в них новые стебли. Концы этих стеблей связывают, и получается окружность, определяющая диаметр мяча.
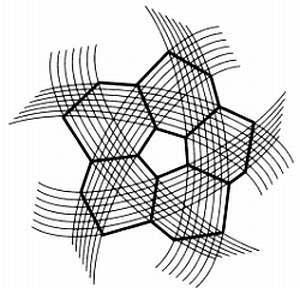
Постепенно по ходу плетения появляются пятиугольные грани — сначала как промежутки между прутьями, которые постепенно заполняются. По сути, полученный мяч по форме представляет собой икосаэдр с отсеченными вершинами — пирамидами с пятиугольным основанием. Разрезав эти пирамиды горизонтально пополам, получим 20 пятиугольных отверстий. Закрыв эти отверстия гранями, имеем полуправильный многогранник — усеченный икосаэдр, имеющий 60 вершин, 90 ребер и 32 грани (20 из них имеют форму шестиугольников, 12 — форму пятиугольников). Именно этот многогранник и плетет мастер. Ротанг распрямляется, и в результате мяч обретает постоянную кривизну. Пересечения трех стеблей из пучков в шесть стеблей определяют 20 шестиугольных граней мяча.
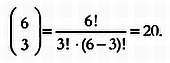
Убедитесь в этом сами.
Японские шары темари имеют китайское происхождение. Изначально их изготавливали из оленьих шкур для придворных, которые использовали темари для игр. Когда придворные дамы начали ткать шары из шелка, темари обрели новую роль и стали использоваться в качестве украшений. Даже проводились конкурсы на лучший шар темари с самым сложным узором и искусным сочетанием цветов.
Искусство плетения шаров темари восходит к 1000 году нашей эры и передается из поколения в поколение, от матери к дочери. Со временем темари становились все более популярными, возникали новые техники их изготовления. С появлением резиновых мячей интерес к темари надолго угас, но сегодня это традиционное искусство вновь обрело былую популярность, и в Японии даже организованы специальные общества, посвященные темари.

Японские шары темари.
В центре темари находится шар из пенопласта или мягкого пластика, куда удобно втыкать булавки. Узоры на ткани шаров преимущественно геометрические и отличаются невероятной сложностью.
При изготовлении шаров темари очень полезной оказывается раздвоенная линейка в форме буквы V с углом раствора в 72°, которая, по сути, представляет собой две линейки с соединенными концами. Этот инструмент нужен потому, что большинство узоров темари представляют собой замощения сферы, основанные на додекаэдре. Это означает, что мастерам нужно работать с правильными пятиугольниками и системой из пяти радиальных осей. Если мы разделим полный круг (360°) на пять частей, то получим угол раствора линейки — 72°.
Одна из первых задач, которую требуется решить при изготовлении темари, касается разделения поверхности шара на восемь равных частей. Для этого нужно воспользоваться основным различием между плоскостью и криволинейной поверхностью, то есть сферой. На плоскости сумма углов треугольника всегда равна 180°, а на сфере она может составлять 270°.
Поверхность темари делится на восемь частей следующим способом. Сначала на шаре булавкой отмечается произвольная точка. Затем вокруг шара оборачивается лента так, что она проходит через отмеченную точку дважды. Далее эта точка отмечается на ленте, и лента обрезается. Так определяется длина окружности шара. Теперь лента складывается пополам так, и на ней отмечается место сгиба. Затем лента сгибается еще раз, и метки ставятся на каждой из ее половин. Таким образом отметки на ленте указывают ее четверть, половину и три четверти длины.