Метод. Московский ежегодник трудов из обществоведческих дисциплин. Выпуск 3: Возможное и действитель - Страница 28

Существует ряд методик сравнения затраченных ресурсов и полученных результатов. Так, к примеру, в экономической оценке государственных программ «конкурентом» упомянутого выше CBA является CEA – Cost-Effectiveness Analysis. CEA основан на сопоставлении альтернативных программ с точки зрения затрат на достижение результата в терминах определенных единиц анализа; например, так называемый «life-years saved» для программ в сфере здравоохранения [Grosse, Teutsch, Haddix, 2007]. В этой работе мы покажем ключевые принципы оценки продуктивности на примере метода Data Envelopment40 Analysis (DEA); в последние годы он приобрел довольно широкое распространение в сравнительных исследованиях эффективности. Как правило, в российской литературе используется оригинальное название метода41, и мы будем следовать этой традиции.

Концептуально подход к оценке эффективности в рамках DEA восходит к классической идее оптимальности по Парето (Парето-эффективности), предполагающей в самом общем виде невозможность увеличения («улучшения») какого-либо параметра без уменьшения («ухудшения») других параметров. Напомним традиционный пример из микроэкономических учебников [см.: Самуэльсон, Нордхаус, 2008, с. 42–46]: в Парето-эффективной экономике невозможно увеличить выпуск одного продукта без снижения выпуска другого. На рис. 1 а отображено множество всех неотрицательных пар значений признаков X (выпуск масла) и Y (выпуск пушек). Он разбивается на два подмножества кривой АС, называемой границей производственных возможностей, ГПВ (product-possibility frontier, PPF). Все комбинации {x, y}, находящиеся выше ГПВ, запрещены, т.е. не могут быть реализованы в рамках данных экономических возможностей. Все множество комбинаций под ГПВ неэффективно, так как допускает так называемое Парето-улучшение: увеличение выпуска одного продукта без снижения выпуска другого. Неэффективному множеству принадлежит, к примеру, точка B на рис. 1 а. Все Парето-эффективные сочетания объемов выпуска находятся на кривой АС.

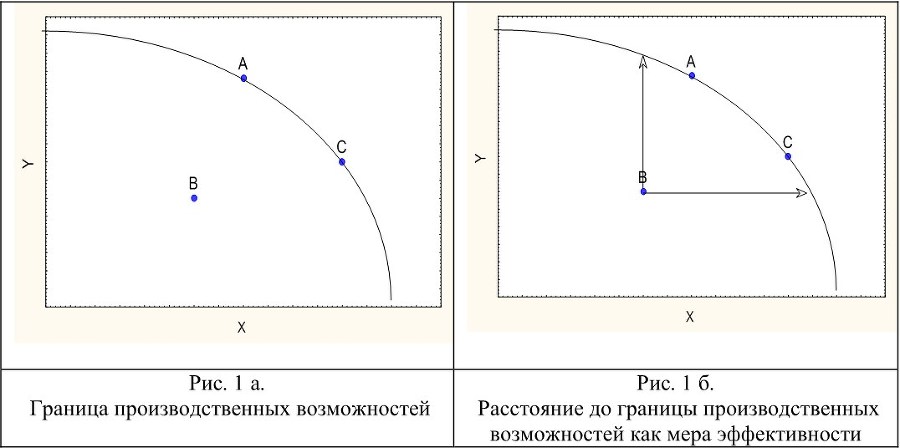
Несмотря на кажущуюся абстрактность этого критерия, он сразу дает ключ к оценке уровня (степени) эффективности. Для DMU, лежащих на кривой производственных возможностей, уровень эффективности по определению равен 1 или 100%. Для DMU под ГПВ эффективность определяется расстоянием до этой границы (рис. 1 б).

Оставаясь в рамках той же логики, мы можем перейти от «пространства продуктов» к пространству «входов и выходов» (рис. 2). По оси OX теперь будет откладываться объем использованного ресурса, по оси OY – количественное выражение полученного результата. Например, будем считать, что X – это государственные расходы на программу повышения квалификации чиновников, а Y – число управленцев, прошедших переподготовку. Точки на плоскости, отражающие различные комбинации затрат и результатов, будут соответствовать DMU – допустим, региональным администрациям (A, B, C, D).

Рис. 2. DMU в пространстве «вход – выход» .

Региональные администрации, соответствующие точкам В и D на рис. 2, неэффективны, так как для них имеется возможность: а) увеличить количество обучаемых чиновников без снижения затрат (D→D’), б) снизить затраты без уменьшения числа обучаемых чиновников (B→B’). В практических задачах прямо различают эффективность, ориентированную на «выход» (output-oriented efficiency), и эффективность, ориентированную на «вход» (input-oriented efficiency). В первом случае (для точки D на рис. 2) эффективность рассчитывается как отношение FD/FD’, во втором (для точки B) – как отношение EB’/EB. Так или иначе, фактический уровень выхода при данном уровне входа сравнивается с максимально возможным в данной системе.

Граница производственных возможностей задается некоторой функцией, которую в самом общем виде можно записать как:

где

– вектор результатов, – вектор ресурсов. Векторное определение x и y подчеркивает тот факт, что DMU может преобразовывать набор различных ресурсов в набор различных результатов (рис. 3). Если мы имеем дело с более чем одним входом и/или более чем одним выходом, ГПВ уже не может быть отображена кривой на плоскости. Корректно будет говорить об этой границе как о поверхности в трехмерном пространстве или гиперповерхности в многомерном пространстве.

Рис. 3.

Преобразование вектора ресурсов в вектор результатов

Важное упрощение, заложенное в модели (1), заключается в предположении, что получаемые результаты зависят только от вложенных ресурсов и степени эффективности DMU. Здесь мы пока не принимаем во внимание тот факт, что даже сравнительно однородные DMU оперируют в различных условиях, которые могут способствовать или противодействовать достижению ГПВ. Например, в регионе с большой территорией и низкой плотностью населения оказание медицинской помощи всегда будет сопряжено с большими затратами ресурсов, в частности с высокими транспортными издержками.

Итак, в модели (1) F выступает в качестве некоторой «эталонной» функции, «траектории» в пространстве ресурсов и результатов, определяющей максимально возможный эффект от затраты данного количества ресурсов в данных условиях, общих для всех DMU. В этом контексте следует особо подчеркнуть, что ГПВ на значительных промежутках времени не статична; она меняется по мере технологического развития, трансформации институционального контекста и др. К примеру, если мы сравниваем эффективность отдельных регионов в сфере образования, ГПВ будет определяться, в частности, качеством федеральной политики в этой области.

В прикладном анализе практическая проблема состоит в нахождении ГПВ – не абстрактной математической функции, а конкретного эталона для оценки конкретных DMU. В сфере разработки инженерных решений ГПВ может быть задана аналитически: благодаря законам, сформулированным в рамках точных наук, можно оценить, к примеру, количество полезной работы, которое может быть в принципе произведено при данных затратах энергии. Для общественных наук этот путь, видимо, закрыт: никто не знает, какое максимальное количество «общественного здоровья» можно «произвести» на истраченный бюджетный рубль. Задача определения ГПВ и, соответственно, оценки эффективности изначально ставится в относительном (или сравнительном) ключе: решение будет справедливо лишь применительно к тому множеству объектов, которые непосредственно включены в анализ. Так, в исследовании региональных систем образования на материале США мы получим некоторый набор штатов, лежащих на ГПВ и имеющих оценку 1. Аналогично на материале субъектов РФ мы также получим набор территорий максимальной эффективности с единичной оценкой. Однако это вовсе не будет означать, что «единичные» штаты эффективны в той же мере, в какой эффективны «единичные» российские регионы, так как границы производственных возможностей будут существенно отличаться. Если объединить североамериканские и российские регионы в рамках одного анализируемого множества, то с формальной математической точки зрения мы получим сопоставимые оценки42. Однако в таком исследовании будет нарушен принцип однородности. В то же время мы можем (по крайней мере в принципе) сравнивать эффективность образования в США, России и еще в целом ряде стран мира, если они будут образовывать единый анализируемый массив.