Магистр Рассеянных Наук - Страница 79

— По этому случаю вернёмся наконец к нашим баранам, — предложил я. — Первым долгом обсудим вопрос Единички: чего больше — натуральных чисел или их квадратов?

— Но Единичка уже ответила на него! — возразила Таня. — И Магистру вряд ли удастся её опровергнуть.

— Между прочим, — напомнил Олег, — этим вопросом мы уже занимались. В прошлом году, когда говорили о множествах…

— А ведь верно! — сказала Таня. — Вопрос Единички и в самом деле касается множеств…

— Притом бесконечных множеств, — уточнил Сева. — И Единичка, конечно же, права: раз каждое число натурального ряда можно возвести в квадрат, значит, квадратов существует ровно столько, сколько натуральных чисел, то есть бесконечное множество.

— Надо сказать, Единичка доказала это очень простым способом, — вмешался я. — Над каждым квадратом она надписала его порядковый номер, то есть попросту пересчитала их. Недаром множества, которые можно перенумеровать, называются счётными.

— А разве есть множества, которые пересчитать нельзя? — спросил Нулик.

— Конечно. Вот, например, множество точек на отрезке прямой. Оно несчётное, хотя количество точек на любых отрезках прямой всегда одинаково.

— Как же так? — прошептал Нулик, окончательно потеряв голос от изумления.

— Вот так. Где, по-твоему, точек больше: на средней линии треугольника или на его основании?

— Что за вопрос! — фыркнул Нулик. — Конечно, на основании! Ведь оно вдвое длиннее средней линии.

— Не угадал. Пусть средняя линия вдвое меньше основания, а точек и тут и там совершенно одинаковое множество.

Я нарисовал треугольник, начертил его среднюю линию и провёл из вершины с десяток лучей, которые пересекли и среднюю линию и основание.

— Как видишь, каждый луч, пересекающий среднюю линию, непременно пересечёт и основание треугольника. Таких лучей я могу провести сколько угодно через любую точку средней линии. А раз так, значит, любой точке средней линии непременно соответствует какая-нибудь точка основания. Стало быть, множество точек и тут и там одинаково. Вот что бывает, когда имеешь дело с бесконечными несчётными множествами. Здесь сплошь да рядом часть равна целому.

— Ну и фокус! — выдохнул Сева.

— В бесконечности такие фокусы — дело обычное.

— Да, с бесконечностью лучше не связываться, — сказал Нулик. — И вообще пора нам отправляться на индульгенцию к вице-губернатору.

— А может, всё-таки на аудиенцию? — подмигнул Сева.

— Все остришь, да зря, — остановила его Таня. — Он ни того, ни другого не знает.

— Ничего, сейчас мы его просветим. Индульгенция, дорогой президент, слово латинское. В прямом значении это милость, а вообще-то так называется у католиков церковная грамота об отпущении грехов. Вот, например, натворил ты что-нибудь и хочешь искупить свою вину. Ступай к священнику да не забудь денег прихватить — и отпущение тебе обеспечено.

— А если денег у меня нет?

— Нет, так и ходи непрощенный.

— Ну и ладно! — неожиданно рассвирепел Нулик. — Не надо мне такой индульгенции!

— Мне тоже, — серьёзно согласился Олег. — Откупаться от грехов деньгами, это не для нас с тобой! Правда, Нулик? Мы люди порядочные. Махнём-ка лучше на приём, то бишь на аудиенцию к губернатору, и займёмся задачей о золотом полукруге.

Но президента, видимо, такая перспектива не слишком устраивала. Он вдруг безмолвно замотал головой, указывая пальцем на своё горло.

— А ещё порядочный человек! — потешалась Таня. — Спорить у него голоса хватает, а как надо задачу решать — так нет его!

Она взяла циркуль, линейку, вычертила на бумаге полукруг и сделала на нём две отметки: одну посередине диаметра, другую посередине полуокружности.

— Явное нарушение! — не выдержал президент. — Во-первых, решать задачу с помощью линейки по условию нельзя, а во-вторых, полукруг должен быть золотой.

— Во-первых, — весело передразнила Таня, — обойдёшься и нарисованным полукругом. Во-вторых, к решению я ещё только приступаю. Значит, так. Требуется отделить от полукруга часть, равновеликую квадрату, сторона которого равна радиусу полукруга.

— А это и есть квадратура круга! — запрыгал на одной ножке Нулик.

— Так думает Магистр, — возразила Таня. — И он, как всегда, неправ. В задаче о квадратуре круга требуется заменить равновеликим квадратом весь круг. Мы же должны заменить квадратом всего лишь часть круга.

— Все равно, — не унимался президент, — значит, это частичная квадратура круга.

— Скорее, наоборот, — поправил я, — не частичная квадратура, а квадратура части круга. И если полный круг заменить равновеликим квадратом немыслимо, то хитро выделенную часть круга в квадрат превратить можно. Это и собирается доказать нам Таня.

Таня отмерила циркулем расстояние от конца диаметра до его середины.

— Все видят, что расстояние между ножками циркуля равно радиусу полукруга? — спросила она.

— Все видят, — сказал Нулик.

Тогда Таня воткнула иглу циркуля в левый конец диаметра и, повернув циркуль против хода часовой стрелки, засекла карандашом небольшую дугу. Потом она вставила иголку в середину полуокружности и тем же радиусом засекла другую дугу, которая пересеклась с первой.

— Теперь смотрите внимательно, — сказала Таня. — Из точки пересечения этих двух дужек тем же раствором циркуля, то есть радиусом полукруга, провожу внутри нашего полукруга дугу. Эта дуга начинается из левого конца диаметра и доходит до середины полуокружности. Таким образом, полукруг разделился на две неравные части, и площадь большей из этих двух частей равна r², то есть равновелика квадрату со стороной, равной радиусу… Пожалей своё горло, Нулик! Я и так знаю, что ты хочешь сказать, и потому прямо перехожу к доказательству.

Таня соединила концы диаметра с серединой полуокружности. Получился равнобедренный треугольник.

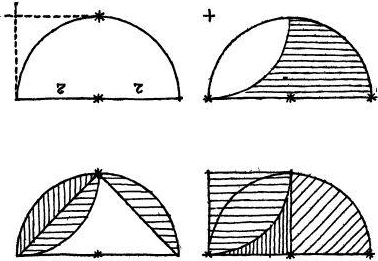
— Доказать, что боковая сторона треугольника разделила меньшую часть полукруга на два равновеликих сегмента, нетрудно. Потому пусть каждый сделает это сам. А теперь посмотрите сюда, на эти три сегмента. Все они образованы боковыми сторонами треугольника, которые одновременно и хорды полукруга. Стало быть, площади этих трех сегментов равны между собой. А раз они равны, значит, треугольник и большая часть полукруга тоже равновелики. Ведь сегмент, отнятый от треугольника слева, прибавляется к этому треугольнику справа! А так как площадь треугольника равна r² (ведь основание у него 2r, высота r, а 2r·¹/₂r=r²), то значит, и площадь искомой нами части полукруга тоже равна r².

— Ловко доказано… — вздохнул Сева.

— Ловко, но длинновато, — заметил Олег. — Я бы доказал это проще.

Он тут же вычертил новый полукруг и циркулем отделил от него ту часть, что полагается. Затем на левой половине полукруга построил квадрат, приняв за сторону вертикальный радиус.

— А теперь смотрите внимательно, — продолжал Олег. — Видите, из каких частей состоят квадрат и отделённая часть полукруга?

— Видим, — прохрипел Нулик. — Они имеют по общей части и… — Тут он запнулся.

— …и по равному сектору — четверти круга, — закончил его мысль Олег.

— Вот именно. А это значит, что большая часть полукруга и квадрат равновелики, — заключил президент и добавил неожиданно чистым голосом: — Что и требовалось доказать.

— Редкий случай в медицине! — заметил Сева. — Лечение геометрией.

— А ведь в самом деле прошло! — радовался Нулик. — Ой, как легко стало! Точно с меня гордиеву петлю сняли…

— Что-то ничего о такой не слыхал, — усмехнулся Сева.

— Как это не слыхал! Почитай письмо Магистра.

— Все равно, нет гордиевой петли. Есть гордиев узел. Такое же иносказательное выражение, как «вернёмся к нашим баранам». Только баранам около четырехсот лет, а узлу более двух тысяч.