Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews - Страница 5
Практически в любом учебнике по общей теории статистики и по эконометрике можно более подробно познакомиться со спецификой уравнений регрессии. (См., например, учебник «Эконометрика» под ред. И.И. Елисеевой. – 2-е изд., пер. и доп. – М,: Финансы и статистика, 2006, стр. 43-132).
Существуют формулы, по которым можно самостоятельно найти параметры, как уравнения линейной регрессии, так и различных видов уравнений нелинейной регрессии. Однако с внедрением в широкую практику компьютеров и соответствующих компьютерных программ уже нет необходимости оценивать параметры уравнения регрессии вручную, тем более что этот процесс довольно трудоемкий.
2.2. Решение уравнения регрессии в Excel с учетом фактора времени. Интерпретация и оценка значимости полученных параметров
Поэтому далее остановимся на изучении алгоритма решения уравнений регрессии с применением соответствующих вычислительных программ. При этом работу с уравнениями регрессии в компьютерных программах можно разделить на три этапа.
На первом, подготовительном этапе необходимо определиться с набором факторов, которые необходимо включить в уравнение регрессии, а также с его аналитической формой, что в ряде случаев требует предварительной обработки данных. Например, в случае выбора степенного уравнения регрессии вместо исходных данных нужно взять их логарифмы.
Второй этап состоит из собственно решения уравнения регрессии и нахождения его параметров.
На третьем этапе проводится оценка и тестирования общего качества уравнения регрессии, проверка статистической значимости каждого из коэффициентов регрессии, определяются их доверительные интервалы, а также принимается окончательное решение об адекватности или неадекватности полученного уравнения регрессии.
Как известно, одним из наиболее распространенных способов определения тренда в динамике курса валюты является построение его зависимости от фактора времени T. Так, если в качестве зависимой переменной Y мы возьмем ежемесячный курс доллара, а в качестве независимой переменной T – время (в данном случае порядковые номера месяцев, начиная с июня 1992 г.=1), то у нас получится следующее уравнение парной линейной регрессии:
Y расч. =a + bT (2.2);
где a – свободный член уравнения регрессии; b – линейной коэффициент регрессии, показывающий, как изменение величины независимой переменной (фактора) T в среднем способствует изменению зависимой переменной (результативного признака) Y; Y расч. – расчетное значение результативного признака, вычисляемое по формуле (2.2).
Минимизируем сумму квадратов отклонений (остатков) Y факт. от Y расч.,то есть от фактических значений курса доллара от его расчетных значений. В результате формулу МНК (2.1.1) для линейной регрессии можно в данном случае представить в виде формулы (2.3):
Уравнение (2.3) в принципе можно решить самостоятельно, если найти его параметры согласно формулам (2.1.4) и (2.1.5), но в целях ускорения этого процесса мы будем его решать с помощью Пакета анализа Excel. Кстати, желающие лучше усвоить суть МНК могут сначала самостоятельно в «ручном режиме» решить данное уравнение регрессии, а затем сверить свои результаты с теми, что мы получим в Excel.
Для того чтобы подготовить исходные данные к решению данного уравнения регрессии разместим в Excel два столбца исходных данных. В первом столбце, который озаглавим Time, поместим порядковые номера месяцев, начиная с июня 1992 г. (с номером =1) и кончая апрелем 2010 г. (с номером =215). Во втором столбце, который озаглавим USDOLLAR, поместим данные по курсу доллара на конец месяца, начиная с июня 1992 г. и заканчивая апрелем 2010 г. (последние данные, имевшиеся на тот момент, когда писались эти строки). Таким образом столбец Time представляет собой независимую переменную, которая в формуле (5) обозначена символом T, а столбец USDOLLAR является зависимой переменной Yфакт. Далее переходим к решению уравнения регрессии в Пакете анализа Excel, о том, как это делается, можно прочитать ниже – в алгоритме действий № 3.
Алгоритм действий № 3 «Как решить уравнение регрессии в Excel»
Шаг 1. Ввод в уравнение исходных данных
Делается это следующим образом: сначала в Microsoft Excel 2007 г. в верхней панели инструментов выбирается опция Данные (в Microsoft Excel 1997-2003 гг. нужно выбрать опцию Сервис), потом в появившемся окне Анализ данных – опция Регрессия. После чего появляется новое окно – Регрессия (см. рис. 2.1), в котором в графе Входной интервал y выделяем (с помощью мышки) столбец данных USDOLLAR (ячейки $C$1:$C$216). Здесь же в графе Входной интервал Х» выделяем столбец данных Time(ячейки $B$1:$B$216), то есть независимую переменную T из нашего уравнения регрессии (5).
Шаг 2. Дополнительные опции
Если бы мы хотели получить уравнение регрессии без свободного члена, который в формуле (2.2) обозначен символом a, то тогда нам следовало бы выбрать еще и опцию КОНСТАНТА-НОЛЬ. Однако в данном случае в использовании этой опции нет необходимости.
Опцию Остатки следует выбирать тогда, когда есть необходимость, чтобы в выходных данных содержалась информация об отклонении расчетных y от их фактических значений. При этом остатки находятся по следующей формуле (2.4):
Остатки = Yрасч.– Yфакт. (7); где Yрасч. – расчетные, Yфакт. – фактические значения результативного признака.
Опцию МЕТКИ применяют для того, чтобы переменные, включенные в уравнение регрессии, в выводе итогов были обозначены в виде заголовков соответствующих столбцов.
По умолчанию оценка в Excel параметров уравнения регрессии делается с 95% уровнем надежности. Однако в случае необходимости в опции Уровень надежности можно поставить цифру 99, что означает задание для программы оценить коэффициенты регрессии с 99% уровнем надежности. В результате в выводе итогов мы получим данные, характеризующие как в целом уравнение регрессии, так и верхние и нижние интервальные оценки коэффициентов данного уравнения с 95% и 99 % уровнями надежности. При 95% уровне надежности существует риск, что в 5 % случаях оценки коэффициентов уравнения регрессии могут оказаться неточными, а при 99% уровне надежности этот риск равен 1%.
Шаг 3. Вывод итогов
На заключительном этапе выбираем в параметрах вывода (окно РЕГРЕСССИЯ) опцию выходной интервал, в которой указываем соответствующую ячейку Excel ($H$2), далее щелкаем по надписи ОК и получаем ВЫВОД ИТОГОВ (см. рис 2.1, где можно увидеть все заданные нами параметры уравнения регрессии). В случае необходимости вывод итогов можно получить на отдельном листе (см. опцию НОВЫЙ РАБОЧИЙ ЛИСТ) или в новой книге Excel (см. опцию НОВАЯ РАБОЧАЯ КНИГА).
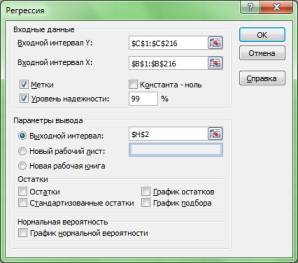
Рис. 2.1. Диалоговое окно РЕГРЕССИЯ для вывода итогов при решении в Excel уравнения регрессии
Результаты решения уравнения регрессии, которые в программе Excel выдаются в виде единой таблицы под заголовком ВЫВОД ИТОГОВ, у нас представлены в виде трех блоков (см. табл. 2.2-2.4). Так, в табл. 2.2 сгенерированы результаты по регрессионной статистике, в табл. 2.3 дается дисперсионный анализ, а в табл. 2.4 оценивается статистическая значимость коэффициентов регрессии .
Параметры, представленные в табл. 2.2, оценивают уровень аппроксимации фактических данных, полученный с помощью данного уравнения регрессии. Так, параметр Множественный R обозначает множественный коэффициент корреляции R, который характеризует тесноту связи между результативным признаком Y и факторами переменными X1, X2…Xn. Данный коэффициент изменяется в пределах от 0 до 1, причем, чем ближе к 1, тем теснее корреляционная связь между переменными, включенными в уравнение регрессии. Множественный коэффициент корреляции равен квадратному корню, извлеченному из коэффициента детерминации R2, который у нас также приводится в регрессионной статистике. Множественный коэффициент R также находят по формуле (2.5):