Искусство схемотехники. Том 1 (Изд.4-е) - Страница 17
Однако можно встретить, например, такое выражение: «импеданс конденсатора на данной частоте составляет…». Дело в том, что в импеданс входит реактивное сопротивление, и поэтому не обязательно говорить «реактивное сопротивление конденсатора», можно сказать и «импеданс конденсатора». На самом деле слово «импеданс» часто употребляют и тогда, когда известно, что речь идет о сопротивлении; например, говорят «импеданс источника» или «выходной импеданс», имея в виду эквивалентное сопротивление некоторого источника. То же самое относится и к «входному импедансу».
В дальнейшем речь пойдет о схемах, для питания которых используется синусоидальный сигнал с определенной частотой. Анализ схем, работающих с сигналами другой формы, требует большей тщательности и предполагает использование уже известных нам методов (например, метода дифференциальных уравнений или метода преобразования Фурье, при котором сигнал представляют в виде ряда синусоид). На практике эти методы редко используются.
1.18. Частотный анализ реактивных схем
Для начала рассмотрим конденсатор, на который подается синусоидальное напряжение источника питания (рис. 1.47).
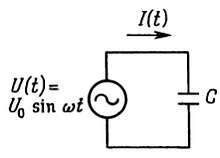
Рис. 1.47.
Ток в схеме определяется следующим образом:
I(t) = C(dU/dt) = C·ω·U0·cos ωt.
Из этого уравнения следует, что ток имеет амплитуду I и опережает входное напряжение по фазе на 90°. Если не принимать во внимание соотношение фаз, то
I = U/(1/ωC).
(Напомним, что ω = 2πf). Конденсатор ведет себя как резистор, сопротивление которого зависит от частоты и определяется выражением R = 1/ωC, и, кроме того, ток, протекающий через конденсатор, сдвинут по фазе на 90° относительно напряжения (рис. 1.48).
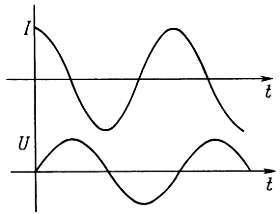
Рис. 1.48.
Например, через конденсатор емкостью 1 мкФ, подключенный к силовой сети с напряжением 110 В (эффективное значение) и частотой 60 Гц, будет протекать ток, эффективная амплитуда которого определяется следующим образом: I = 110/[1/(2π·60·10-6)] = 41,5 мА (эффективное значение).
Замечание: сейчас нам необходимо воспользоваться комплексными переменными; при желании вы можете пропустить математические выкладки, приводимые в последующих разделах, и принять на веру полученные результаты (они выделены в тексте). Не думайте, что подробные алгебраические преобразования, приводимые в этих разделах, необходимы для понимания всего остального материала книги. Это не так - глубокое знание математики похвально, но совсем не обязательно. Следующий раздел, пожалуй, наиболее труден для тех, у кого нет достаточной математической подготовки. Но пусть это вас не огорчает.
Определение напряжения и тока с помощью комплексных чисел. Только что вы убедились в том, что в цепи переменного тока, работающей с синусоидальным сигналом некоторой частоты, возможен сдвиг по фазе между напряжением и током. Тем не менее если схема содержит только линейные элементы (резисторы, конденсаторы, индуктивности), то амплитуда токов на всех участках схемы пропорциональна амплитуде питающего напряжения. В связи с этим можно попытаться найти некоторые общие выражения тока, напряжения и сопротивления и обобщить тем самым закон Ома.
Очевидно, что для того, чтобы определить ток в какой-либо точке схемы, недостаточно задать одно значение-дело в том, что ток характеризуется как амплитудой, так и сдвигом фазы.
Конечно, можно определять амплитуды и фазовые сдвиги напряжений и токов явно, например U(t) = 23,7·sin(377·t + 0,38), но оказывается, что проще это делать с помощью комплексных чисел. Вместо того чтобы тратить время и силы на сложение и вычитание синусоидальных функций, можно легко и просто складывать и вычитать комплексные числа. Так как действующие значения напряжения и тока представляют собой реальные количественные величины, изменяющиеся во времени, следует вывести правило для перевода реальных количественных величин в комплексное представление и наоборот. Напомним еще раз, что мы имеем дело с частотой синусоидального колебания ω, и сформулируем следующие правила:
1. Напряжение и ток представляются комплексными величинами U и I.
Напряжение U0cos(ωt + φ) представляется комплексным числом U0ejφ. Напомним, что ejθ = cos θ + jsin θ, где j = √—1.
2. Для того чтобы получить выражение для действующего напряжения и тока, нужно умножить соответствующие комплексные представления на ejωt и выделить действительную часть. Это записывается следующим образом: U(t) = Re(U·ejωt), Ι(t) = Re(I·ejωt). Иначе говоря,

(В электронике символ j используется вместо принятого в алгебре для комплексной переменной символа i, с тем чтобы избежать путаницы с током, который также обозначают символом i). Итак, в общем случае действующие напряжения и токи определяются следующим образом:
U(t) = Re(U·ejωt) = Re(U)·cos ωt — Im(U)·sin ωt,
Ι(t) = Re(I·ejωt) = Re(I)·cos ωt — Im(I)·sin ωt,
Например, комплексному напряжению U = 5j соответствует реальное напряжение
U(t) = Re[5j·cos ωt + 5j(j)·sin ωt] = 5sin ωt B
Реактивное сопротивление конденсаторов и индуктивностей. Принятое соглашение позволяет применять закон Ома для схем, содержащих как резисторы, так и конденсаторы, и индуктивности.
Определим реактивное сопротивление конденсатора и индуктивности. Нам известно, U(t) = Re(U0·ejωt). Так как в случае конденсатора справедливо выражение I = C(dU/dt), получим
Ι(t) = — U0Cω·sin ωt = Re[U0·ejωt/(-j/ωC)] = Re(U0·ejωt/XC),
т. е. для конденсатора
XC = — j/ωC,
ХC — это реактивное сопротивление конденсатора на частоте ω. Конденсатор емкостью 1 мкФ, например, имеет реактивное сопротивление —2653j Ом на частоте 60 Гц и —0,16j Ом на частоте 1 МГц. Для постоянного тока реактивное сопротивление равно бесконечности. Аналогичные рассуждения для индуктивности дают следующий результат:
XL = jωL.
Схема, содержащая только конденсаторы и индуктивности, всегда обладает мнимым импедансом; это значит, что напряжение и ток всегда сдвинуты по фазе друг относительно друга на 90°- схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть. Под реактивным сопротивлением подразумевается при этом только мнимая часть импеданса.
Обобщенный закон Ома. Соглашения, принятые для представления напряжений и токов, позволяют записать закон Ома в следующей простой форме:
I = U/Z, U = I·Z, означающей, что напряжение U, приложенное к схеме с импедансом Z, порождает ток I. Импеданс последовательно и параллельно соединенных элементов определяется по тем же правилам, что и сопротивление последовательно и параллельно соединенных резисторов: