Искатели необычайных автографов или Странствия, приключения и беседы двух филоматиков - Страница 4

Мате внезапно остановился и с интересом уставился на проходившего мимо человека в высокой шапке.

— Взгляните-ка, Фило, вот так колпак!

— Парфянский, — мгновенно определил тот. — Помните, у Пушкина? «Узнаю коней ретивых по их выжженным таврам, узнаю парфян кичливых по высоким клобукам…» Кстати, знаете вы, что Хорасан — родина наших Хайямов — был в древности центром Парфянского государства?

— К сожалению, нет, — сказал Мате. — Зато наверняка знаю, что судьба свела меня с человеком сведущим и умным.

— Взаимно, взаимно, — любезно ответствовал Фило. — У Хайяма есть на этот счет прекрасные стихи. Хотите послушать?

«Ну, попался!» — подумал Мате, но отказаться все-таки не посмел (не та была минута!), только спросил опасливо:

— А они длинные?

— Побойтесь Бога! — застонал Фило, прижимая пальцы к вискам. — По-моему, даже грудные младенцы знают, что Хайям писал четверостишия. Между прочим, по-персидски «четверостишие» — «рубай».

Мате обреченно вздохнул, рубай так рубай. Не в том суть. Главное, что стихи, как он понял, о преимуществе дружбы с умным человеком. Фило сказал, что так оно и есть, и прочитал внятно и с выражением:

Ну как?

Мате растерялся. Он с изумлением заметил, что четверостишие очень ему понравилось, но сознаться в этом не желал из упрямства. К счастью, упрямства в нем было все-таки меньше, чем прямоты.

— Поразительно! — произнес он после недолгой борьбы с самим собой. — Какая краткость и какая точность! Это напоминает изящную математическую формулу.

С его стороны это была высшая похвала, но Фило она озадачила: формула — и вдруг изящная? Мате, наверное, шутит…

— А вы, разумеется, считаете, что изящным может быть только произведение искусства, — напустился на него Мате, к которому сразу вернулась вся его язвительность. — Где вам понять, что и формула может быть многословной и краткой, неуклюжей и отточенной, путаной и прозрачной, тяжеловесной и воздушной! Где вам знать, что есть формулы стройные, а есть хромые, совсем как стихи; мелкие и глубокие — как мысли; узкие и всеобъемлющие — как духовный кругозор… Клянусь решетом Эратосфена, формулой можно выразить все! Да, да, все, и по-разному. И пожалуйста, не возражайте! Иначе вы заставите меня пожалеть о том, что я назвал вас умным человеком.

Но Фило не собирался возражать. Он вдруг закрыл глаза и стал медленно поводить носом из стороны в сторону.

— В чем дело? — спросил Мате довольно резко.

— Разве вы не знаете, что при закрытых глазах обостряется обоняние?

— В первый раз слышу.

— А вы зажмурьтесь. Чувствуете? О боги, какое благоухание! Интересно, чем это пахнет?

— Прозрейте и посмотрите направо, — насмешливо посоветовал Мате.

Фило посмотрел и замер: в нескольких шагах от него на низкой жаровне лежала стопка румяных маслянистых лепешек. Рядом на корточках восседал их владелец и привычным голосом выпевал:

— А вот лепешки, сдобные лепешки! С пылу, с жару, по дирхему[5] за пару!

— Есть у нас дирхем, Мате?

Тот подбросил на ладони несколько полтинников выпуска 1965 года.

Фило нетерпеливо облизнул губы.

— Что же делать?

— Обменять полтинники на дирхемы, что же еще? Где-то была тут лавчонка менялы…

Сгорбленный кривоглазый старик в полосатом тюрбане и засаленном халате долго вертел между скрюченными пальцами незнакомые монеты.

— Испанские? — спросил он наконец, сверля диковинных чужеземцев единственным, неестественно выпученным глазом.

Мате отрицательно покачал головой.

— Венецейские?

— Российские, — сказал Мате, уверенный, что меняла ни за что не захочет сознаться в своем невежестве.

Он не ошибся: поторговавшись для приличия (ибо какой уважающий себя финансист совершает сделки не торгуясь?), старый скупердяй отсыпал им горсть звонких монеток, и скоро друзья снова очутились подле жаровни с лепешками. Фило выбрал одну порумяней и поднес ко рту, но Мате остановил его.

— Неужели вы действительно собираетесь съесть эту лепешку? — спросил он с сожалением.

— А что же с ней еще делать? Носить на груди вместо медальона?

— Отчего бы и нет! У нее такая совершенная форма. Идеальное коническое сечение.

— Ну и пусть комическое, мне-то что! — нетерпеливо отмахнулся Фило и разом отхватил половину лепешки.

— Да не комическое, а ко-ни-чес-ко-е! Неужели вы никогда не читали знаменитого трактата о конических сечениях, написанного великим древнегреческим математиком Аполлонием Пергским?

Мате прекрасно понимал, что трактата Аполлония Фило и в глаза не видал, — просто ему хотелось пристыдить своего спутника. Но тот и не думал смущаться.

— Не угнетайте меня, пожалуйста, своей эрудицией, — заявил он независимо. — Еще Хайям учил: «Будь мягче к людям! Хочешь быть мудрей, — не делай больно мудростью своей!»

Мате очень хотелось ответить, что вовсе не он, а Фило угнетает его своей эрудицией. Но вместо того он молча вытащил из кармана потрепанный блокнот, вырвал из него листок бумаги, свернул кулечком и, аккуратно подогнув края, поставил к себе на ладонь.

— Как по-вашему, что это такое?

— Фунтик! — по-детски обрадовался Фило.

— Сами вы фунтик! — добродушно огрызнулся Мате. — Конус это. Круговой конус, то есть такой, у которого основание — круг. И, как у всякого порядочного кругового конуса, есть у него вершина и ось. Иначе говоря, перпендикуляр, опущенный из вершины на основание. Заметьте еще, что окружность основания называется направляющей, а прямая, которая соединяет вершину конуса с любой точкой этой окружности, — образующей конуса. Понимаете?

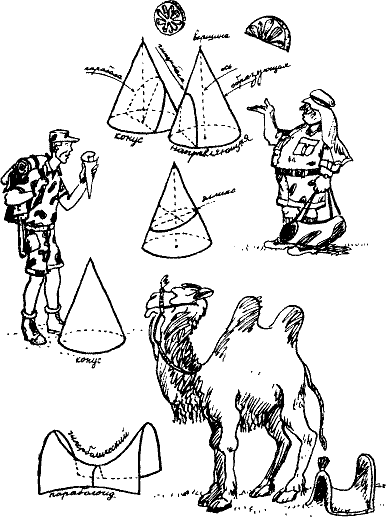
Фило неуверенно кивнул.

— Теперь возьмем плоскость, — не унимался Мате.

— Где возьмем?

— О Господи! В воображении, конечно. Итак, возьмем воображаемую плоскость и рассечем ею конус, ну, хотя бы параллельно оси. В этом случае на поверхности конуса появится линия, которая называется гиперболой. Видите?

Но нет, Фило ничего не видел.

— Полное отсутствие математического воображения, — констатировал Мате и карандашом нарисовал на поверхности фунтика кривую от воображаемого сечения.

— Вот вам гипербола. А теперь рассечем конус параллельно образующей. При этом на поверхности его получится линия, которая называется параболой. Вот она.

Фило отрывисто засмеялся.

— Интересно, как вы отличаете гиперболу от параболы? На мой взгляд, они совершенно одинаковы.

— Так то на ваш взгляд. А на самом деле…

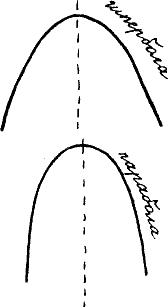
Мате снова достал блокнот и быстро начертил две кривые.

— Неужели вы и теперь не замечаете никакой разницы?

— Теперь замечаю, — снизошел Фило. — У гиперболы концы расходятся как у рогатки, а у параболы вроде бы держатся поближе, словно что-то их пригибает или притягивает друг к другу… Но при чем тут все-таки лепешки?

— Не беспокойтесь, дойдем и до лепешек, — заверил Мате. — На сей раз проведем такое сечение, которое не будет ни параллельным образующей, ни параллельным оси. В общем, нечто промежуточное между ними. И как вы думаете, что у нас при этом получится? У нас получится замкнутая кривая, которая называется эллипсом.

— Лепешка! — сейчас же установил Фило, взглянув на контур, нарисованный на фунтике. — Как сказано в «Евгении Онегине», увы, сомнений нет, я съел эллипс!

— Теперь никто не упрекнет вас в том, что вы не пробовали геометрии… Но шутки в сторону. На этом маленьком примере я хотел показать вам, что все на свете может быть выражено языком математики.