Хаос. Создание новой науки - Страница 16
Ознакомительная версия. Доступно 16 страниц из 77.Впрочем, экологи давно уже поняли, что им необходимо нечто более сложное. Ученый, наблюдая за рыбами в реальном водоеме, должен постараться найти функцию, которая учитывала бы жестокую реальность, например угрозу голода или соперничество в стае. По мере роста популяции истощается запас пищи. Размеры небольшой стаи быстро растут, а чересчур большая сокращается. Возьмем жуков-вредителей. Попробуйте каждый год первого августа подсчитывать их численность в вашем саду. Чтобы упростить задачу, не принимайте во внимание птиц, болезни данного вида насекомых — учтем лишь имеющийся запас пищи. Выяснится, что жуки активно размножаются, когда их мало, но стоит им чересчур расплодиться, как они объедят весь сад и после этого погибнут от голода.
В мальтузианской схеме неограниченного увеличения численности популяции значение линейной функции роста всегда будет увеличиваться. Схема же, более приближенная к жизни, должна включать в себя особый фактор, сдерживающий рост, если популяция уже и так велика. Наиболее подходящей кажется функция, которая будет резко возрастать при небольших размерах популяции, сводить рост ее численности примерно к нулю при средних размерах и снижаться при быстром размножении особей. Пользуясь ею из раза в раз, эколог может наблюдать, как ведет себя популяция на протяжении длительных периодов времени, и придать своей модели определенную стабильность. Позаимствовав все необходимое из математики, эколог будет рассуждать примерно так: «Мы имеем уравнение. Вот переменная, являющаяся коэффициентом воспроизводства. Вот другая — коэффициент естественной смертности. Третья переменная служит коэффициентом смертности, обусловленной внешними причинами, в том числе голодом и нападением хищников. И вот, смотрите: популяция будет расти с такой-то скоростью, пока не достигнет такого-то уровня равновесия».
Но как найти подобную функцию? Могут подойти многие уравнения. Простейшей модификацией, пожалуй, окажется линейная зависимость, предложенная Мальтусом: х с = rх(1- x). Как и выше, величина rявляется коэффициентом роста, который можно увеличить или уменьшить. Новый член (1- x) удерживает рост в определенных границах, т. е. когда хвозрастает, 1- xуменьшается [3]. Имея калькулятор, можно задать начальное значение, выбрать коэффициент роста и вычислить результат — численность популяции в следующем году.
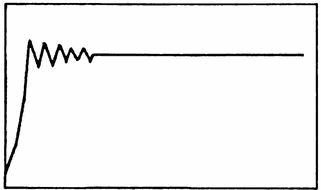
Рис. 3.1. Популяция достигает равновесия после роста, чрезмерного увеличения численности особей и ее снижения.
К 50-м годам экологи уже использовали варианты рассмотренного выше уравнения, известного как логистическое разностное уравнение. В частности, В.-Е. Рикер из Австралии применил его для оценки рыбных промыслов. Ученые поняли, что коэффициент роста rявляется важной характеристикой модели. В физических системах, откуда, собственно, и позаимствовала экология подобные уравнения, данный параметр отвечал количеству теплоты, или силе трения, или другим физическим величинам, порождаемым хаотическим движением, — словом, количеству нелинейности. Применительно к рыбным угодьям он должен соответствовать плодовитости рыб, колебанию численности популяции в обоих направлениях (что именуется биотическим потенциалом). Вопрос заключался в том, каков механизм влияния различных факторов на дальнейшую судьбу изменяющейся популяции. Очевидно, что более низкое значение параметра повлечет за собой стабилизацию числа особей на относительно невысоком уровне, а то, что повыше, приведет к стабилизации на более высоком уровне. Это справедливо для многих величин, но отнюдь не для всех. Некоторые исследователи, и Рикер в их числе, применяли величины, имевшие достаточно высокие значения, и, осуществляя опыты, разглядели хаос.
Кажется удивительным, что поведение ряда показателей, поддающихся измерению и исчислению, обнаруживает определенные странности, досадные для любого, кто работает с ручной вычислительной машинкой. Конечно, бесконтрольный рост чисел еще не наблюдается, но нет и стабильности. Впрочем, ни один из ученых 60-х годов не был склонен (а может, не хватало упорства) продолжать вычисления до тех пор, пока искомая упорядоченность не будет найдена. Так или иначе, колебания численности популяции дали экологам повод предположить, что происходят они около некоего скрытого уровня равновесия. Считая последнее весьма важным, экологи ни в коем случае не предполагали, что этого уровня может не быть.
Справочники и учебники, посвященные логистическим уравнениям и их более сложным вариантам, не содержали, как правило, никаких указаний на проявления неупорядоченности. Дж. Мэйнард Смит в своей классической работе «Математические идеи в биологии», вышедшей в 1968 г., так определил возможные перспективы развития: численность популяции часто является величиной постоянной, или же отклонения случаются «весьма регулярно» в области предполагаемой точки равновесия. Автор не был столь наивен, чтобы допускать отсутствие хаотичного элемента в жизни реальных популяций. Он лишь полагал, что с описанными им математическими моделями хаос не имеет ничего общего. Будь это иначе, биологи избегали бы пользоваться подобными моделями. Если модель не оправдывала ожиданий своего создателя относительно реального положения дел в популяции, расхождение всегда можно было объяснить тем, что какая-то величина (возрастной состав популяции, специфика ареала обитания или географической среды, соотношение полов) осталась неучтенной.
Чаще всего неупорядоченность числового ряда ученые списывали на несовершенство счетной машинки. Интерес представляли стабильные решения, устойчивость казалась лучшей наградой. В конце концов, процедура подбора нужных уравнений и их решения требовала известных усилий. Никто не хотел впустую тратить время на ошибочные изыскания, не выявлявшие стойкой тенденции, и ни один опытный исследователь не забывал, что его уравнения не более чем примитивная версия реальных событий. На упрощения шли ради моделирования упорядоченности. Стоило ли преодолевать трудности, чтобы узреть хаос?
Говорят, что идеи Лоренца по-настоящему открыл Джеймс Йорк и он же дал науке о хаосе ее нынешнее имя. Вторая часть этого утверждения справедлива.
Йорк был математиком, но предпочитал считаться философом, хотя это и таило в себе некоторую опасность. Остроумный и велеречивый, с всклокоченной шевелюрой, он обожал кроткого, но беспокойного Стива Смэйла. Подобно многим, Йорк признавал, что понять Смэйла непросто. Однако в отличие от большинства коллег он знал, почему же так трудно постичь логику Стива. Двадцати двух лет от роду Йорк поступил в Физико-технологический институт при Мэрилендском университете, который сам же позже и возглавил. Он относился к числу тех математиков, которые во что бы то ни стало стремятся претворить свои идеи в жизнь, чтобы они принесли пользу. Написанный им доклад о распространении гонореи убедил федеральные власти в необходимости изменения стратегии контроля за заболеваемостью. Во время топливного кризиса 70-х годов он выступил в суде штата Мэриленд с весьма корректными (но не слишком убедительными) аргументами в пользу того, что ограничение отпуска бензина лишь усугубит ситуацию. Когда в эпоху антивоенных выступлений правительство опубликовало снятые с самолета-шпиона фотографии — редкие группки людей вокруг памятника Вашингтону в разгар акции протеста, — Йорк проанализировал фотографию и по форме тени, отбрасываемой изваянием, установил, что в действительности снимок был сделан на полчаса позже, когда митингующие уже расходились.
Работая в институте, Йорк наслаждался возможностью трудиться над вопросами, выходящими за привычные рамки, и постоянно консультироваться со множеством представителей других дисциплин. Как-то одному из них, посвятившему себя изучению динамики жидкостей, попалась на глаза статья Лоренца «Детерминистский непериодичный поток», написанная в 1963 г. С тех пор минуло девять лет. Будучи очарован работой Лоренца, физик вручал копии статьи всем, до кого удавалось дотянуться. В числе прочих копию получил и Йорк.