Хаос. Создание новой науки - Страница 13
Ознакомительная версия. Доступно 16 страниц из 77.Хотя гипотеза Смэйла не подтвердилась, она дала новое направление его исследованиям сложных динамических систем. Ряд математиков по-новому оценили возможности осциллятора ван дер Поля. Смэйл приложил их выводы к неизвестной области. Единственным его осциллографом был мозг, но этот мозг довели до совершенства годы изучения топологической Вселенной. Смэйл досконально разобрался в спектре активности осциллятора, в его, по выражению физиков, фазовом пространстве. Любое состояние системы, зафиксированное в определенный момент времени, раскрывалось в одной точке фазового пространства. Все данные о положении или скорости системы содержались в координатах указанной точки. По мере изменения системы точка меняла свои координаты в фазовом пространстве, вычерчивая траекторию.
Фазовое пространство простой системы, вроде маятника, вероятно, представляет собой прямоугольник. Угол колебаний маятника в заданный момент времени определяет положение точки на оси восток — запад, а его скорость — на оси север — юг. Для маятника, стабильно качающегося взад и вперед, траектория в фазовом пространстве напоминает петлю, закручивающуюся вновь и вновь, по мере того как система раз за разом проходит через те же состояния.

Рис. 2.1. Построение изображений в фазовом пространстве. Традиционные временные последовательности (вверху)и траектории в фазовом пространстве (внизу)используются как два вида наглядного отображения одних и тех же данных и поведения системы в течение длительного периода времени. Первая (слева)система сходится в одной точке фазового пространства, что подразумевает стабильное состояние. Вторая периодически повторяет саму себя, образуя циклическую орбиту. Третья также обнаруживает периодическое повторение, но в более сложном, «вальсовом» ритме, демонстрируя цикл с тремя волнами. Четвертая хаотична.
Вместо того чтобы наблюдать за траекторией, Смэйл сосредоточился на изучении целостного пространства в момент изменения системы, например во время увеличения движущей силы. При этом он сконцентрировал свои размышления на некой геометрической сущности, абстрагировавшись от сути физической. Смэйл анализировал топологические трансформации в фазовом пространстве, т. е. такие преобразования, как растяжение и сжатие. Иногда эти преобразования несли в себе прямой физический смысл. Так, рассеивание и потеря энергии на трение наглядно отображались тем, что очертания системы в фазовом пространстве сжимались, словно опадающий воздушный шар, сокращаясь в итоге до точки, в которой система окончательно останавливалась. Смэйл понял, что для воспроизведения всей неупорядоченности осциллятора ван дер Поля в фазовом пространстве необходимо использовать новый комплексный набор трансформаций, и быстро превратил идею о зрительном представлении глобального поведения системы в неизвестную ранее модель. Его изобретение — овладевший умами образ хаоса — представляло собой структуру, известную под названием подковы.
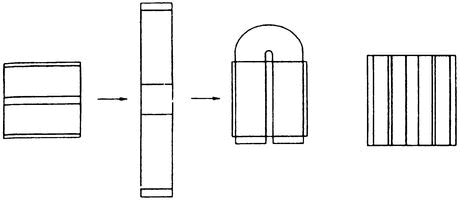
Рис. 2.2. Подкова Смэйла. Такая топологическая трансформация заложила весьма простую основу толкования хаотичных свойств динамических систем: пространство растягивается в одном направлении, сжимается в другом, а затем перегибается. При повторении операции образуется нечто вроде структурированного беспорядка, подобного тому, который мы получаем, сворачивая пирожные из слоеного теста. Две точки, оказавшиеся рядом в конце преобразований, вначале могли находиться далеко друг от друга.
Чтобы представить себе упрощенный вариант подковы Смэйла, вообразите прямоугольник, а затем совместите верхнюю и нижнюю его стороны. Получится брусок, который надо согнуть буквой «С», а потом выровнять концы, чтобы получилась подкова. Подкову нужно встроить в новый прямоугольник и повторить преобразования: сжатие, свертывание и выравнивание.
Описанная выше процедура напоминает работу кондитера, который ловко растягивает сладкую жирную массу, сворачивает ее вдвое, вновь вытягивает, и так снова и снова, пока конфета не приобретет изящную продолговатую форму и сахарные завитки внутри нее не станут повторять друг друга самым причудливым образом. Смэйл создал свою подкову, минуя несколько стадий топологического преобразования. Отвлекшись от математики, можно отметить, что подкова — точный и зримый образ «сильной зависимости от начальных условий», которую Лоренц откроет несколькими годами позже. Выберите две соседние точки в начальном пространстве — и не угадаете, где именно они окажутся после сгибания и скручивания пространства.
Первоначально Смэйл надеялся объяснить поведение всех динамических систем с помощью операций вытягивания и сжатия, не прибегая к сгибанию, по крайней мере к такому, которое сильно подорвало бы устойчивость системы. Однако это преобразование оказалось необходимым и дало возможность описать резкие перемены в динамическом поведении объекта. Подкова Смэйла стала первой в ряду новых геометрических форм, благодаря которым математики и физики многое узнали о движении. Это изобретение — детище топологии, а не физики — казалось несколько искусственным для прикладных целей, однако оно послужило отправным пунктом для дальнейших изысканий. В 60-е годы Смэйл создал в Беркли исследовательскую группу из молодых математиков, разделявших его взгляд на нетрадиционное изучение динамических систем. Прошло десятилетие, прежде чем результаты их работы удостоились внимания представителей других, не столь далеких от практики дисциплин. Когда это все же случилось, физики поняли, что Смэйл повернул целый раздел математики лицом к реальному миру, и заговорили о наступлении золотого века науки.
«Происходит самая эпохальная смена парадигм из всех, какие я видел» — так прокомментировал происшедшее Ральф Абрахам, коллега Смэйла, впоследствии профессор математики в отделении Калифорнийского университета.
«Когда я начал свою профессиональную деятельность в сфере математики в 1960 г., совсем не так давно, последняя в современном ее варианте полностью — именно полностью— отвергалась даже самыми передовыми физиками, прибегавшими в своих исследованиях к математике. Дифференциальная динамика, глобальный анализ, разнообразные виды планирования, дифференциальная геометрия — почти всё предали забвению, и это лишь через пару лет после открытий Эйнштейна, высоко ценившего математическую науку! Можно сказать, что брак между математикой и физикой завершился разводом уже в 30-х годах — ученые двух областей, ничего не обсуждая между собой, презирали друг друга. Матфизики (а встречались и такие) не позволяли своим выпускникам посещать занятия математиков: Оставьте математику! Мы сами научим вас всему, что нужно знать. Они лишь извратят ваше мышление!Тогда шел 1960 год. Через восемь лет ситуация коренным образом изменилась». Физики, астрономы, биологи — все осознавали, что стоят на пороге новых открытий.
Одна из загадок космоса — Большое Красное Пятно на Юпитере. Овальной формы, огромное, оно кружится, словно гигантский вихрь, и никогда не останавливается… Взглянув на снимки, переданные «Вояджером-2», каждый узнает хорошо знакомое проявление турбулентности, правда, невиданного доселе, вселенского масштаба. Пятно — одна из давно известных достопримечательностей Солнечной системы, «налитое кровью око средь завитков нахмуренных бровей», как описал его Джон Апдайк. Но что же это такое? Через двадцать лет после Лоренца Смэйл и другие ученые, по-новому взглянув на различного свойства природные токи, поняли, что атмосфера Юпитера подбрасывает им загадку, достойную того, чтобы на ней испытать возможности науки о хаосе. Три столетия подряд лучшие умы бились над разгадкой этой тайны, но чем больше узнавали, тем меньше понимали. Астрономы обнаружили Пятно вскоре после того, как Галилей направил свои телескопы на крупнейшую из планет Солнечной системы. Роберт Хук увидел это образование еще в начале XVII века, Крети изобразил таинственный феномен на полотне (работа хранится в картинной галерее Ватикана). Окраска Пятна проясняла не многое. Однако телескопы совершенствовались, и новое знание порождало новые гипотезы и теории, буквально наступавшие на пятки друг другу. Вот лишь некоторые из них.