Физика учит новый язык. Лейбниц. Анализ бесконечно малых - Страница 13

1/2+(1/2)²+(1/2)³+(1/2)⁴+ ... + 1/2+1/4+1/8+1/16+ ...= 1

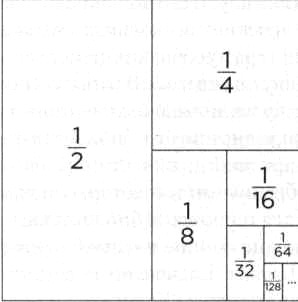
Этот процесс нагляден: возьмем за единицу площадь квадрата, который мы разделим на две части, и одну из них — снова напополам; из двух оставшихся частей одна снова делится посередине, и теоретически можно продолжить данный процесс до бесконечности. Суммой всех полученных нами фигур является исходный квадрат, то есть единица. С этим типом рядов, которые обычно представлены следующим выражением:

∑rⁿ = 1+r+r²+r³+r⁴+...

^n≥0

знакомы и работают ученики средней школы. Чтобы найти значение суммы, нам нужно сложить п членов геометрической прогрессии, а затем умножить эту сумму на знаменатель прогрессии г. Затем вычитаем одно выражение из другого:

S = (1+r+r²+r³+r⁴+...+rⁿ)- (r • S = r+r²+r³+r⁴+r⁵+...+rⁿ⁺¹)/(S - r • S = 1 - rⁿ⁺¹)

Таким образом мы можем выделить S и получить значение суммы, которое мы искали:

S = (1-rⁿ⁺¹)/(1-r)

Теперь, если принять, что r имеет значение, меньшее 1, и что вместо сложения п членов мы складываем бесконечное количество, значение rn⁺¹ становится нулем, и, следовательно, сумма сводится к:

S = 1/(1-r)

Математики всегда искали формулы, которые бы позволили с легкостью складывать большое число членов. Уже в античности были известны суммы членов рядов первых степеней: n, n² и n³.

1+2+3+4+5+6+7+...+ = n(n+1)/2 = n²/2+n/2,

1²+2²+3²+...+n² = n(n+1)(2n+1)/6 = n³/3+n²/2+n/6,

1³+2³+3³+...+n³ = n²(n+1)²/4 = n⁴/4+n³/2+n²/4.

Но с самого начала математики были очень заинтересованы в изучении конкретного случая, когда сумма бесконечного числа членов дает конечное значение. Над этой проблемой работали, например, Демокрит и Архимед.

На основе геометрического ряда

∑rⁿ

^n≥1

в Средние века исследовали ряды степеней, в которых менялись местами основание и показатель степени, например:

∑n^r

^n≥1

Вскоре было замечено: если показатель степени r положительный, а n — целое число, сумма превращается в бесконечность. Когда показатель степени r отрицательный, получаются степени дробей, меньших единицы, то есть сумма

∑(1/n)^r, где r больше единицы.

^n≥1

Французский математик Николай Орезмский (1323— 1382) получил много результатов, исследуя ряды, и первым доказал, что гармонический ряд, то есть ряд, составленный из членов, обратных числам натурального ряда, для r = 1 является расходящимся. Следовательно, сумма большого числа членов стремится к бесконечности. В то время доказательства приводили в буквальном виде, описывая шаги, которые нужно сделать, но мы рассмотрим это искусное рассуждение, пользуясь более привычными символами. Орезмский сгруппировал члены, то есть у него был первый член, два следующих, четыре следующих, восемь следующих и так далее:

1/2+1/3+1/4+1/5+1/6+1/7+1/8+...+ = 1/2+(1/2+1/4)+(1/5+1/6+1/7+1/8)+...+ = 1/2+7/12+533/840+...

Так получается ряд дробей, каждая из которых больше 1 /2, то есть сумму ряда можно сделать больше любого указанного числа, просто взяв достаточное число членов ряда.

Индийский математик и астроном Мадхава из Сангамаграма (1350-1425) описал среди прочих бесконечных рядов ряды тригонометрических функций синуса и косинуса. Он также нашел ряд арктангенса:

arct x = x - x³/3 + x⁵/5 + x⁷/7 + ,,,

Через несколько лет шотландский математик Джеймс Грегори (1638-1675) первым в Европе открыл этот ряд, о нем узнал Лейбниц и воспользовался им для выведения первого ряда для числа π, недостатком которого было то, что он очень медленно приближается к истинному значению. Он известен как ряд Грегори — Лейбница, хотя другие авторы сегодня его называют рядом Мадхавы — Лейбница:

π/4 = 1 - 1/3 + 1/5 + 1/7 + ... + (-1)ⁿ/(2n+1) + ...

И Ньютон, и Лейбниц также вычисляли ряды степеней других тригонометрических функций.

Вычисление числа k было постоянным предметом поиска математиков всех времен. Это число определяется как отношение между длиной окружности и ее диаметром. Многие пытались найти наибольшее количество десятичных знаков данного числа, и одним из использованных методов был метод числовых рядов. Он подразумевает, что по мере того, как вычисляется больше членов, появляется большее количество точных знаков после запятой.

Ряды не всегда были суммами. Например, математик Франсуа Виет (1540-1603), один из создателей современной алгебры, представил первое бесконечное произведение, приближающееся к значению π, таким образом:

π = 2 • 2/√2 • 2/√(2+√2) • 2/√(2+√(2+√2)) • 2/√(2+√(2+√(2+√2)))

Сам Грегори, в свою очередь, пытаясь вычислить площадь круга, пришел к другому выражению для вычисления я:

π/2 = (2 • 2 • 4 • 4 • 6 • 6 • 8 • 8 ...)/(1 • 3 • 3 • 5 • 5 • 7 • 7 • 9 ...)

XVII век был временем популярности сумм бесконечных рядов степеней, которые служили для поиска квадратуры фигур, ограниченных различными типами кривых, то есть площади сегмента какой-либо кривой.

ЛЕЙБНИЦ И БЕСКОНЕЧНЫЕ РЯДЫ

Когда в 1672 году Лейбниц навестил Гюйгенса в Париже, он рассказал ему о методе, над которым работал. Он использовался для нахождения суммы членов бесконечных рядов чисел и состоял в том, чтобы учитывать разность между членами последовательности. Если у нас есть ряд членов a₀<а₁<а₂<а₃<... a_n, то возьмем разности b₁= a₁-a₀; b₂= а₂-а₁; b₃= а₃-а₂; ..., и тогда нулевая сумма а₀-а₀ + а₁ - а₁ + а₂ - а₂ +...+ a_n-1 - a_n-1 + + a_n - a_n = а₀ + b₁ + b₂ +...+ b_n - a_n = 0, откуда следует, что сумма разностей равна:

b₁ + b₂ + b₃ + ... + b_n = a_n - a₀

Лейбниц утверждал, что его метод разностей может быть применен для нахождения суммы любого ряда чисел, построенного в соответствии с правилом, и даже для бесконечных рядов — при условии, что они сходятся.

На той же встрече Гюйгенс задал Лейбницу задачу, которую он сам уже решил, чтобы тот проверил свой метод, — найти сумму чисел, обратных треугольным, то есть следующий ряд:

1 + 1/3 + 1/6 + 1/10 + ...

Лейбниц разделил на два каждый член, разложив дроби на разность двух:

1/2+1/6+1/12+1/20+...+1/2+(1/2-1/3)+(1/3-1/4)+(1/4-1/5)+...+1/2+1/2 = 1

следовательно, значение искомой суммы членов данного ряда составляет 2(1 + 1).

Также Лейбниц сформулировал то, что известно как теорема сходимости знакочередующихся рядов, то есть рядов, в которых чередуются складываемые и вычитаемые члены. В основном это выражение вида:

_∞

∑(-1)ⁿ • a_n = a₀ - a₁ + a₂ - a₃ + a₄ - ... при a_n ≥ 0.

ⁿ⁼⁰

Данный критерий впервые появился в письме, адресованном Иоганну Бернулли (1667-1748) в 1713 году.