Физика для всех. Молекулы - Страница 30
Силы сопротивления при больших скоростях
Но вернемся к законам "мокрого" трения. Как мы выяснили, при малых скоростях сопротивление зависит от вязкости жидкости, скорости движения и линейных размеров тела. Рассмотрим теперь законы трения при больших скоростях. Но прежде надо сказать, какие скорости считать малыми, а какие большими. Нас интересует не абсолютная величина скорости, а то8 является ли скорость достаточно малой, чтобы выполнялся рассмотренный выше закон вязкого трения.
Оказывается, нельзя назвать такое число метров в секунду, чтобы во всех случаях при меньших скоростях были, применимы законы вязкого трения. Граница применения изученного нами закона зависит от размеров тела и от степени вязкости и плотности жидкости.
Для воздуха "малыми" являются, скорости меньше
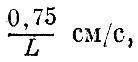
для воды - меньше
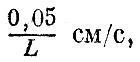
а для вязких жидкостей, вроде густого меда, - меньше
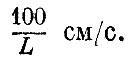
Таким образом, к воздуху и особенно к воде законы вязкого трения мало применимы: даже при малых скоростях, порядка 1 см/с, они будут годиться лишь для крошечных тел миллиметрового размера. Сопротивление, испытываемое ныряющим в воду человеком, ни в какой степени не подчиняется закону вязкого трения.
Чем же объяснить, что при изменении скорости меняется закон сопротивления среды? Причины надо искать в изменении характера обтекания жидкостью движущегося в нем тела. На рис. 6.3 изображены два круговых цилиндра, движущихся в жидкости (ось цилиндра перпендикулярна к чертежу). При медленном движении жидкость плавно обтекает движущийся предмет - сила сопротивления, которую ему приходится преодолевать, есть сила вязкого трения (рис. 6.3, а). При большой скорости позади движущегося тела возникает сложное запутанное движение жидкости (рис. 6.3, б). В жидкости то появляются, то пропадают различные струйки, они образуют причудливы фигуры, кольца, вихри. Карта на струек все время меняется. Появление этого движения, называемого турбулентным, в корне меняет закон сопротивления.

Рис. 6.3
Турбулентное сопротивление зависит от скорости и размеров предмета совсем иначе, чем вязкое: оно пропорционально квадрату скорости и квадрату линейных размеров. Вязкость жидкости при этом движении перестает играть существенную роль; определяющим свойством становится ее плотность,- причем сила сопротивления пропорциональна первой степени плотности жидкости (газа). Таким образом, для силы F турбулентного сопротивления справедлива формула .
F ~ ρν2L2,
где ν - скорость движения, L - линейные размеры предмета и ρ - плотность среды. Числовой коэффициент пропорциональности, который мы не написали, имеет различные значения в зависимости от формы тела.
Обтекаемая форма
Движение в воздухе, как мы говорили выше, почти всегда "быстрое", т. е. основную роль играет турбулентное, а не вязкое сопротивление. Турбулентное сопротивление испытывают самолеты, птицы, парашютисты. Если человек падает в воздухе без парашюта, то через некоторое время он начинает падать равномерно (сила сопротивления уравновешивает вес), но с весьма значительной скоростью, порядка 50 м/с. Раскрывание парашюта приводит к резкому замедлению падения - тот же вес уравновешивается теперь сопротивлением купола парашюта. Так как сила сопротивления пропорциональна скорости движения и размеру падающего, предмета в одинаковой степени, то скорость упадет во столько раз, во сколько изменятся линейные размеры падающего тела. Диаметр парашюта около 7 м, "диаметр" человека около одного метра. Скорость падения уменьшается до 7 м/с. С такой скоростью можно безопасно приземлиться.
Надо сказать, что задача увеличения сопротивления решается значительно легче, чем обратная задача. Уменьшить сопротивление автомобилю и самолету со стороны воздуха или подводной лодке со стороны воды - важнейшие и нелегкие технические задачи.
Оказывается, что, изменяя форму тела, можно уменьшить турбулентное сопротивление во много раз. Для этого надо свести к минимум турбулентное движение, являющееся источником сопротивления. Это достигается приданием предмету специальной, как говорят, обтекаемой формы.
Какая же форма является в этом смысле наилучшей? На первый взгляд кажется, что телу надо придать такую форму, чтобы вперед. двигалось острие. Такое острие, как кажется, должно с наибольшим успехом "рассекать" воздух. Но, оказывается, важно не рассекать воздух, а как можно меньше потревожить его, чтобы он очень плавно обтекал предмет. Наилучшим профилем движущегося в жидкости или газе тела является форма, тупая спереди и острая сзади[4]. При этом жидкость плавно стекает с острия, и турбулентное движение сводится к минимуму. Ни в коем, случае нельзя направлять острые углы вперед, так как острия вызывают образование турбуленлного движения.
Обтекаемая форма крыла самолета создает не только наименьшее сопротивление движению, но и наибольшую подъемную силу, когда обтекаемая поверхность стоит наклонно вверх к направлению движения. Обтекая крыло, воздух давит на него в основном в направлении, перпендикулярном, к его плоскости (рис. 6.4). Понятно, что для наклонного крыла эта сила направлена вверх.

Рис. 6.4
С возрастанием угла подъемная сила -растет. По рассуждение, основанное на одних лишь геометрических соображениях, привело бы нас к неверному выводу, что чем больше угол к направлению движения, тем лучше. На самом же деле по мере увеличения угла плавное обтекание плоскости все затрудняется, а при некотором значении угла, как это иллюстрирует рис. 6.5, возникает сильная турбулентность; сопротивление движению резко возрастает, и подъемная сила падает.

Рис. 6.5
Исчезновение вязкости
Очень часто, объясняя какое-нибудь явление или описывая поведение тех или иных тел? мы ссылаемся на знакомые примеры. Вполне понятно, говорим мы, что этот предмет движется каким-то образом, ведь и другие тела движутся по тем же правилам. Большей частью всегда удовлетворяет объяснение, которое сводит новое к тому, что нам уже встречалось в жизни. Поэтому мы не испытывали особых трудностей, объясняя читателю законы, по которым движутся жидкости,- ведь каждый видела как течет вода, и законы этого движения кажутся вполне естественными.
Однако есть одна совершенно удивительная жидкость, которая не похожа ни на какие другие жидкости, и движется она по особым, только ей свойственным законам. Это жидкий гелий.
Мы уже говорили, что жидкий гелий сохраняется как жидкость при температуре вплоть до абсолютного нуля. Однако гелий выше 2 К (точнее, 2,19 К) и гелий ниже этой температуры -- это совсем разные жидкости. Выше двух градусов свойства гелия ничем не выделяют его среди других жидкостей. Ниже этой температуры гелий становится чудесной жидкостью. Чудесный гелий называют гелием II.
Самое поразительное свойство гелия II - это открытая П. Л. Капицей в 1938 г. сверхтекучесть, т. е. полное отсутствие вязкости.
Для наблюдения сверхтекучести изготовляется сосуд, в дне которого имеется очень узкая щель - шириной всего лишь в полмикрона. Обычная жидкость почти не просачивается сквозь такую щель; так ведет себя и гелий при температуре выше 2,19 К. Но едва только температура становится ниже 2,19 К, скорость вытекания гелия скачком возрастает по крайней мере в тысячи раз. Через тончайший зазор гелий II вытекает почти мгновенно, т. е. полностью теряет вязкость. Сверхтекучесть гелия приводит к еще более странному явлению. Гелий II способен сам "вылезать" из стакана или пробирки, куда он налит. Пробирку с гелием II помещают в дьюаре над гелиевой ванной. "Ни с того ни с сего" гелий поднимается по стенке пробирки в виде тончайшей совершенно незаметной пленки и перетекает через край; с донышка пробирки капают капли.