Фейнмановские лекции по физике. 8. Квантовая механика I - Страница 6

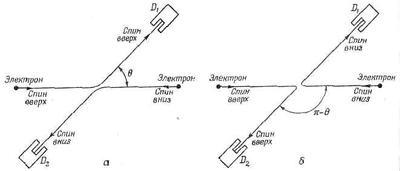
Фиг. 1.9. Рассеяние электронов с антипараллельными спинами.

Эти две возможности показаны на фиг. 1.9; в принципе они различимы, и поэтому интерференции не получится, просто сложатся две вероятности. Все это верно и тогда, когда оба первоначальных спина перевернуты, т. е. если спин слева смотрит вниз, а спин справа — вверх.

Таблица 1.1 · рассеяние неполяризованных частиц со спином ¹/₂

Наконец, если электроны вылетают случайно (например, они вылетают из накаленной вольфрамовой нити полностью неполяризованным пучком), то с равной вероятностью каждый отдельный электрон вылетит либо спином вверх, либо спином вниз. Если мы не собираемся в нашем опыте измерять в ка­кой-нибудь точке спин электронов, то получается то, что назы­вают экспериментом с неполяризованными частицами. Результат этого эксперимента лучше всего подсчитать, перечислив все мыс­лимые возможности, как это сделано в табл. 1.1. Для каждой различимой альтернативы отдельно подсчитана вероятность. Тогда полная вероятность есть сумма всех отдельных вероят­ностей. Заметьте, что для неполяризованных пучков результат при q=p/2 составляет половину классического результата для независимых частиц.

Поведение тождественных частиц приводит ко многим ин­тересным следствиям; в следующей главе мы обсудим их по­подробнее.

* Вообще-то направление рассеяния должно, конечно, описываться двумя углами — полярным углом j и азимутом q. Тогда следовало бы ска­зать, что рассеяние кислорода в направлении (q,j) означает, что a-частица движется в направлении (p-q, j+p). Однако для кулоновского рассеяния (и многих других случаев) амплитуда рассеяния не зависит от j. Тогда амплитуда того, что кислород полетел под углом 6, совпадает с ам­плитудой того, что a-частица полетела под углом (p-q).

* По-русски, наверно, правильнее говорить амплитуда вероятности, но короче говорить просто амплитуда и примириться с выражением типа «амплитуда того, что электрон находится в точке х».— Прим. ред.

* В американском издании этот том начинается с двух глав из второго тома [гл. 37 и 38 (вып. 3)], кото­рые авторы считали нужным повторить. Это было сде­лано для того, чтобы третий том можно было чи­тать, не обращаясь к прежним томам. В русском издании мы не стали печатать их снова: читатель должен всегда держать первые выпуски под рукой, поэтому нумерация глав в русском издании сдвинута на 2 единицы по сравнению с третьим томом. Из тех же соображений мы не перепечатали вновь гл. 34 и 35, они вошли в вып. 7.— Прим. ред.

 

 

Глава 2

ТОЖДЕСТВЕННЫЕ ЧАСТИЦЫ

§ 1.Бозе-частицы и ферми-частицы

§ 2.Состояния с двумя бозе-частицами

§ 3.Состояния с n бозе-частицами

§ 4.Излучение и поглощение фотонов

§ 5.Спектр абсолютно черного тела

§ 6.Жидкий гелий

§ 7.Принцип запрета

Повторить: гл. 41 (вып. 4) «Броуновское движение» (об излучении абсолютно черного тела гл. 42 (вып 4 «Применения кинетической теории»

§ 1. Бозе-частицы и ферми-частицы

В предыдущей главе мы начали рассматри­вать особые правила, по которым происходит с интерференция в процессах с двумя тождественными частицами. Тождественными мы счи­таем такие частицы, которые, подобно электро­нам, никак невозможно отличить друг от друга. Если в процессе имеются две тождественные частицы, то замена той, которая повернула к счетчику, на другую — это неотличаемая альтернатива, которая, как и во всех случаях неотличимых альтернатив, интерферирует с первоначальным случаем, когда обмена не было. Амплитудой события тогда служит сумма двух интерферирующих амплитуд, и существенно, что в одних случаях интерференция происходит в фазе, а в других — в противофазе.

Представим, что сталкиваются две частицы а и b и частица а рассеивается в направлении 1, а частица b — в направлении 2 (фиг. 2.1, а).

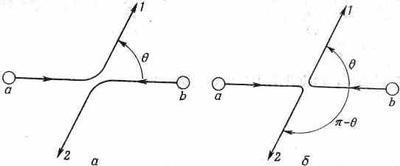
Фиг. 2.1. При рассеянии двух тождественных частиц процессы а и б неразличимы.

Пусть f(q) будет амплитуда этого процесса; тогда вероятность Р₁наблюдения подобного события пропорциональна |f(q)|². Конечно, могло случиться, что частица b рассеялась в счетчик 1, а частица а направилась в счетчик 2 (фиг. 2.1, б). Если считать, что никаких спе­циальных направлений, определяемых спином или чем-то подобным, в опыте нет, то вероят­ность Р₂ этого события можно просто записать в виде | f(p-q)|², потому что этот процесс попросту эквивалентен первому процессу, в котором счетчик 1 поставили под углом (я — 6). И вам могло бы показаться, что амплитуда вто­рого процесса равна просто f(p-q). Но это не обязательно так, потому что в ней мог стоять произвольный фазовый множитель. Иначе говоря, амплитуда могла бы быть такой:

Ведь и такая амплитуда все еще приводит к вероятности Р₂, равной |f(p-q)|².

Посмотрим теперь, что случается, если частицы a и b оказы­ваются идентичными. Тогда два разных процесса, показанных на двух частях фиг. 2.1, уже нельзя друг от друга отличить. Существует амплитуда того, что а или b попадает в счетчик 1, тогда как оставшаяся частица попадает в счетчик 2. Эта амплитуда есть сумма амплитуд двух процессов, показанных на фиг. 2.1.

Если первую мы обозначим f(q), то вторая будет

и теперь уже фазовый множитель очень важен, потому что мы собираемся складывать амплитуды. Предположим, что мы обязаны умножать амплитуду на некий фазовый множитель всякий раз, когда две частицы обмениваются ролями. Если они еще раз обменяются ими, то множитель появится еще раз. Но при этом мы снова возвратимся к первому процессу. Фазовый множитель, взятый дважды, должен вернуть нас к тому, с чего мы начали,— его квадрат должен быть равен единице. Есть только две возможности:

равно либо +1, либо -1. Обмен при­водит ко вкладу в амплитуду с тем же знаком или ко вкладу с противоположным знаком. И оба случая встречаются в природе, каждый для своего класса частиц. Частицы, интерферирующие с положительным знаком, называются бозе-частицами, а те, которые интерферируют с отрицательным знаком, именуются ферми-частицами. Ферми-частицы — это электрон, мюон, оба нейтрино, нуклоны и барионы. Стало быть, амплитуда рассеяния тождественных частиц имеет вид для бозе-частиц:

(Амплитуда процесса)+(Амплитуда обмена); (2.1) для ферми-частиц:

(Амплитуда процесса)-(Амплитуда обмена). (2.2)

Для частиц со спином (скажем, электронов) возникает добавочное усложнение. Нужно указывать не только местопо­ложение частиц, но и направление их спинов. Только в том случае, когда частицы идентичны и их спиновые состояния тоже идентичны, только тогда при обмене частицами амплитуды ин­терферируют. А если вас интересует рассеяние неполяризован­ных пучков, являющихся смесью различных спиновых состоя­ний, то нужны еще выкладки и сверх этого.

Интересная проблема возникает при наличии двух или больше тесно связанных частиц. К примеру, в a-частице сидят четыре частицы: два нейтрона и два протона. И когда рассеи­ваются две a-частицы, может представиться несколько возмож­ностей. Может случиться, что при рассеянии обнаружится ко­нечная амплитуда того, что один из нейтронов перескочит от одной a-частицы к другой, а нейтрон из другой a-частицы пе­рейдет к первой, так что две a-частицы после рассеяния оказы­ваются не первоначальными частицами — произошел обмен парой нейтронов (фиг. 2.2).