Эврика! Радость открытия. Архимед - Страница 16

РИС. 1

РИС. 2
Архимед продолжил удваивать число углов дальше и в конце концов дошел до многоугольника с 96 сторонами! Это позволило ему доказать, что значение площади круга лежит между 3+10/71 и 3+1/7:
«Окружность любого круга составляет три его диаметра и еще менее 1/7 и более 10/71 его части» («Об измерении круга», утверждение 3):
3 + 10/71 < Sc <3 + 1/7, то есть, 3,1408 < Sc < 3,14029.
Таким образом, площадь круга с радиусом 1 составит 3,14, с точностью до двух знаков после запятой. Тут важно отметить: Архимед знал, что он вывел неточное значение. Ведь помещая площадь между двумя разными значениями, ученый прекрасно понимал, что выполняет только приближение.

Согласно еще одному интересному рассуждению, которое можно найти в трактате «Об измерении круга», площадь вписанного в квадрат круга относится к площади этого квадрата как 11/14. И в данном контексте мы тоже приходим к тому же значению π — приблизительно 3,14. Рассмотрим следствие из этого положения. Во- первых, давайте внимательнее посмотрим на чертеж справа.
Площадь круга: Sкруга = πr².
Площадь квадрата: Sквадрата = (2r)²=4r².
Соотношения, которые их связывают:
площадь круга/площадь квадрата = πr²/4r² = π/4
То, что выяснил Архимед:
площадь круга/площадь квадрата = 11/14
Очевидно, что это одна и та же величина, и мы помним, что все выкладки Архимеда приблизительны:
π/4 ~ 11/14 ~ 3.14
В трактате «Об измерении круга» утверждается:
Каждый круг равен прямоугольному треугольнику, один из катетов которого равен радиусу круга, а другой — длине окружности.
Имеется в виду равенство их площадей. Для доказательства (см. рисунок) ученый приводит следующие соображения.
— «Предположим, что площадь круга больше площади треугольника: Sкруга > Sтреугольника». Архимед показывает, что такое неравенство невозможно.
— «Предположим, что площадь круга меньше площади треугольника: Sкруга < Sтреугольника». Архимед доказывает, что невозможно и это.
— Учитывая, что площадь круга не может быть ни меньше, ни больше площади треугольника, они должны быть равны: Sкруга = Sтреугольника.

Пользуясь нынешним алгебраическим языком, вышесказанное можно доказать гораздо легче:
— Sкруга = πr².
— Sтреугольника = (основание • высота)/2 = 2πr*r/2 = πr²
— Что означает: Sкруга = Sтреугольника.
Пусть это изобразят на моем надгробии!
В утверждении 34 трактата «О шаре и цилиндре» содержится результат, которым, как нам точно известно, более всего гордился Архимед:
Соотношение объемов цилиндра и вписанного в него шара равно 3/2. Соотношение площадей поверхности цилиндра и вписанного в него шара также равно 3/2 (см. рисунок):
Vцилиндра 3/2 Vшара
Sцилиндра = 3/2 Sшара
Он смог найти абсолютно точное отношение между объемами шара и цилиндра, в который тот вписан. Речь идет о случае, когда диаметр шара равен как диаметру основания цилиндра, так и его высоте. Объем цилиндра получается в полтора раза (3/2) больше объема шара. Такое же соотношение и у площадей их поверхностей. Как мы уже говорили, Архимед даже завещал выбить изображение шара, вписанного в цилиндр, на своем надгробном памятнике вместо эпитафии. В I веке до н. э. Цицерону, по его словам, удалось увидеть это надгробие. До нашего времени оно, к сожалению, не дошло.

РИС.З
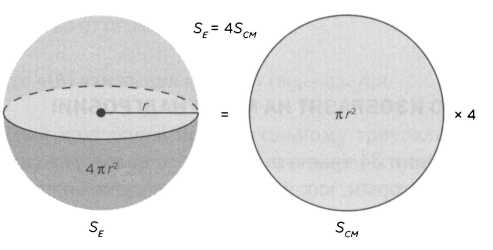
РИС. 4
Чтобы получить нужный результат, Архимед использовал различные определения, постулаты и утверждения, попутно найдя важные соотношения площадей других фигур. «О шаре и цилиндре» — это трактат, состоящий из двух книг, написанных в разные годы его жизни. Первая книга служит теоретической основой для второй, представляющей собой ответы на вопросы Досифея, которому она и посвящена. Первая книга заключает в себе 44 утверждения, шесть определений и пять постулатов. Кроме того, некоторые утверждения содержат важные следствия: например, рассматриваемое соотношение между шаром и цилиндром представлено в форме следствия из двух утверждений. Речь идет об утверждениях 33 и 34.
«Утверждение 33. Поверхность любого шара в четыре раза больше площади его большого круга» (рисунок 4).
Большой круг — это круг, который делит шар на две равные половины. Данное утверждение (рисунок 4) можно пояснить следующим умозрительным образом. Если мы сложим четыре раза площадь SCM большого круга (SCM= πr²), то сумма будет равна площади поверхности всего шара SE (SE = 4πr²). Это означает, что потребовалось бы равное количество краски, чтобы покрасить поверхность шара и четыре больших круга.
«Утверждение 34. Любой шар [по объему] в четыре раза больше конуса, база которого равна большому кругу, а высота — радиусу шара».
В алгебраической записи показать данное соотношение объемов можно так (рисунок 5). Объем Vc конуса с радиусом r и высотой r равен
Vc = 1/3πr³
а объем шара VE с радиусом r равен
VE=4/3πr³.
Таким образом: VE = 4 Vc. То есть объем шара с радиусом r равен объему четырех конусов с радиусом основания r и высотой r. Другими словами, чтобы наполнить весь шар с радиусом r 4 л воды, потребуются 4 конуса с радиусом r и высотой r, вмещающие по 1 л каждый.
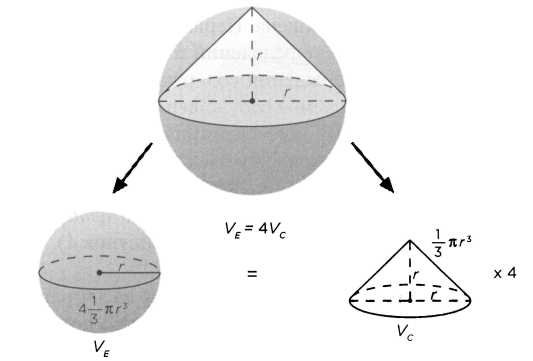
РИС. 5

РИС. 6
В качестве следствия из утверждения 34 Архимед выводит заключение, упомянутое в начале главы и действительное для объемов и площадей:
«Поверхность шара составляет 3/2 поверхности цилиндра с основанием, равным большому кругу шара, и высотой, равной его диаметру» (рисунок 6).
Чтобы вычислить площадь поверхности цилиндра, надо сложить площади его боковой поверхности и двух оснований. Боковая поверхность равна по площади прямоугольнику с основанием 2кг и высотой 2r. Следовательно, ее площадь будет составлять 4πr².
С другой стороны, два основания представляют собой круги с радиусом г, так что площадь каждого равна πr². Сложив площади боковой поверхности и удвоенную площадь основания, получаем площадь поверхности цилиндра: Sc = 6πr².
Итак, из расчетов следует, что площадь цилиндра равна шести площадям круга с таким же радиусом. И значит, один шар равен четырем кругам, а шесть кругов — полутора шарам. Нам понадобится одинаковое количество краски, чтобы покрасить шесть кругов радиусом r, полтора шара радиусом r или один цилиндр с радиусом основания r и высотой 2r. Надо прибавить, что полученные отношения действительны также и для объемов, то есть объем цилиндра составляет 3/2 объема вписанного в него шара (рисунок 7).
Легче и нагляднее представить себе это соотношение следующим образом: если один шар вмещает 2 л воды, то в описанный вокруг него цилиндр войдет 3 л.