Есть идея! - Страница 5
При этом вы сдвинете с места 100 стаканчиков. Предложенное профессором Квибблом шуточное решение позволяет вдвое уменьшить число стаканчиков, сдвигаемых с места.
Существует одна классическая головоломка, очень похожая на только что рассмотренную нами задачу, но несколько более трудную. Начнем с 2n предметов, выстроенных в ряд. Пусть по-прежнему n предметов, составляющих первую половину ряда, будут одного типа, а n предметов, составляющих вторую половину ряда, будут другого типа. (Как и прежде, их можно «моделировать» стаканчиками, фишками, игральными картами и т. п.) Требуется переместить предметы так, чтобы предметы одного типа чередовались с предметами другого типа, но в отличие от предыдущей задачи слову «переместить» придается строго определенное значение. На этот раз слово «переместить» означает, что любые два соседних предмета разрешается, не изменяя их последовательности, изъять из ряда и пристроить к любому свободному концу (после одного или нескольких ходов ряд может распасться на несколько звеньев).
Вот как это делается, например, при n = 3:

Как выглядит общее решение? При n = 1 решение тривиально. При n = 2 задача, как нетрудно выяснить, неразрешима. При всех n > 2 головоломка допускает решение не менее чем за n ходов.
Найти решение при n = 4 не так-то просто, и поиск его, несомненно, доставит вам немало удовольствия. Может быть, вам удастся сформулировать алгоритм решения головоломки за n ходов при любом n > 3.
Не меньший вызов любознательному читателю таят в себе многие необычные варианты той же головоломки. Приведем лишь некоторые из них.
1. Правила перемещения пар остаются теми же за одним исключением: если пара образована предметами различных типов, то перед тем, как пристроить ее к свободному концу, последовательность предметов в паре следует изменить. Например, перемещая две фишки, первая из которых (левая) красная, а вторая (правая) черная, их необходимо поменять местами, после чего первой станет черная, а второй красная фишка, и лишь после этого пристраивать к свободному концу. При 8 фишках существует решение в 5 ходов. При 10 фишках 5 ходов также оказывается достаточно. Общее решение неизвестно. Может быть, вам удастся найти его.
2. Правила такие же, как в исходной задаче, но фишек одного цвета на 1 меньше, чем другого, то есть фишек одного цвета n, а фишек другого n + 1. Доказано, что при любом n задачу можно решить за n² ходов, причем это число минимально.
3. Имеются фишки трех различных цветов. Пары соседних фишек перемещаются по обычному правилу с тем, чтобы фишки каждого цвета оказались выстроенными подряд. При n = 3 (всего 9 фишек) существует решение в 5 ходов. И в этом, и во всех предыдущих вариантах головоломки предполагается, что после последнего перестроения фишки стоят в ряд «сомкнутым строем» (без пробелов). Если ряд может содержать пробелы, то существует необычное решение всего лишь в 4 хода.
Напрашиваются и другие варианты головоломки. Насколько известно, их никто ранее не предлагал и уж конечно не решал. Например, в каждом из приведенных нами вариантов головоломки за один ход можно перемещать не по две, а по три (и более) соседние фишки.
Что произойдет, если на первом ходу переместить фишку, на втором — 2 фишки, на третьем — 3 фишки и т. д.? Если в ряд выстроены n фишек одного цвета и затем п фишек другого цвета, то всегда ли правильного чередования цветов можно добиться за n ходов?
Дороги, которые мы выбираем
Маленькая Сьюзен в большом затруднении. Дело в том, что по дороге в школу ее то и дело подстерегает скверный мальчишка Станки.
Станки. Эй, Сьюзен! Можно, я пойду с тобой?
Сьюзен. Нет, очень тебя прошу, уйди!
Сьюзен. Я придумала, что мне делать. Буду ходить в школу каждое утро другой дорогой. Тогда Станки ни за что не догадается, где меня можно подстеречь.

На этой карте показаны все улицы между домам Сьюзен и ее школой. Направляясь в школу по намеченному маршруту, Сьюзен идет либо строга на восток, либо на юг.
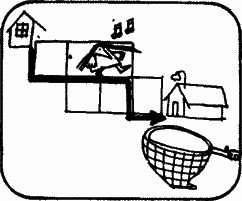
Здесь вы видите Сьюзен, идущую в школу по другой дороге. Разумеется, ей не хотелось бы удаляться от школы. Сколькими способами можно добраться от дома Сьюзен до школы?

Сьюзен. Хотела бы я знать, сколько различных дорог ведет от моего дома к школе. Подумаем! Сосчитать их, должно быть, не просто. Впрочем… Есть идея! Сосчитать дороги совсем не трудно! Очень даже просто!
Какая идея пришла в голову Сьюзен?
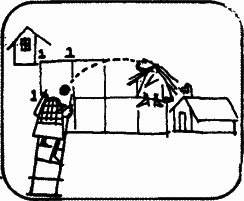
Вот как она рассудила.
Сьюзен. У того перекрестка, возле которого я живу, поставлено на карте число 1: выйти из дома я могу лишь одним способом. У перекрестков, расположенных в одном квартале к востоку и к югу от дома, я поставлю по 1, потому что до каждого из них можно добраться только одним способом.

Сьюзен. У этого перекрестка я поставлю число 2, так как к нему от моего дома ведут 2 различные дороги.
Тут Сьюзен стало ясно, что число у каждого перекрестка равно либо ближайшему числу (если оно одно), либо сумме двух ближайших чисел.

Сьюзен. Еще четыре перекрестка пометила числами. Скоро закончу.
Не поможете ли вы Сьюзен? Не подскажете ли ей, сколько различных дорог ведет от ее дома к школе?
Три перекрестка на ближайшей вертикали справа следует пометить (сверху вниз) числами 1, 4, 9, а два перекрестка на следующей вертикали — числами 4 и 13. Число 13, стоящее на карте у самого правого нижнего перекрестка, показывает, что Сьюзен может выбрать кратчайшую дорогу в школу 13 различными способами.
Придуманный Сьюзен метод действительно приводит к простому и эффективному алгоритму для определения числа кратчайших путей, ведущих от ее дома к школе. Если бы Сьюзен попыталась вычертить все пути, чтобы затем пересчитать их, то решение оказалось бы весьма громоздким, а при большом числе улиц просто необозримым. Вы сможете лучше оценить эффективность предложенного Сьюзен алгоритма, если вычертите все 13 путей.

Чтобы проверить, насколько глубоко вы усвоили алгоритмы Сьюзен, попробуйте нарисовать сети улиц, имеющие другие конфигурации, и подсчитать число кратчайших путей, ведущих из точки А в точку В. Четыре задачи этого типа представлены на рис. 1. Решать их можно по-разному, например, воспользоваться комбинаторными формулами, но все методы несколько сложнее алгоритма Сьюзен.
Чему равно число кратчайших путей, по которым ладья может перейти из одного углового поля на шахматной доске в другое, диагонально противоположное? Эта задача легко решается, если каждому полю на шахматной доске приписать по числу так же, как Сьюзен приписывала числа перекресткам на карте города. Ладья ходит только по горизонтали и вертикали. Следовательно, кратчайший путь из любой клетки в любую другую состоит в преодолении разделяющего клетки расстояния по горизонтали и по вертикали. Если числа расставлены верно (см. рис. 2), то они указывают число кратчайших путей, ведущих из нижнего угла в любое поле. Например, поле в правом верхнем углу помечено числом 3432. Следовательно, ладья может перейти с поля, стоящего в левом нижнем углу доски на диагонально противоположное поле 3432 кратчайшими путями.