Есть идея! - Страница 47
Интересные варианты той же идеи возникают, если вместо кружков взять числа. Требуется разделить квадрат прямыми на части так, чтобы в каждой части числа обладали каким-нибудь общим отличительным свойством. Свое искусство в решении задач этого типа вы можете испытать на следующей головоломке (рис. 5). Требуется провести 4 прямые так, чтобы они разделили квадрат на 11 частей и сумма чисел в каждой части была равна 10. Решение этой задачи приведено в конце книги.

Невразумительное объявление

Проф. Слог. Даю вам еще один шанс выиграть 6 коробок сигар. В одном городке на витрине небольшой гостиницы с рестораном красовался такой плакат.

Проф. Слог. Но когда несовершеннолетние юнцы зашли в ресторан и потребовали спиртные напитки, их вышвырнули вон.

Проф. Слог. По словам владельца гостиницы, художник, написавший плакат, пропустил два восклицательных знака. Расставьте их так, чтобы текст плаката обрел тот смысл, который хотел вложить в него хозяин гостиницы, человек строгих правил и безупречной репутации.

Мистер Рите не справился и с этим заданием. Проф. Слогу пришлось самому расставить восклицательные знаки.
Во многих старинных сборниках забав и развлечений можно найти примеры фраз, смысл которых существенно зависит от того, как расставлены знаки препинания. Вспомним хотя бы знаменитый пример с телеграммой «КАЗНИТЬ НЕЛЬЗЯ ПОМИЛОВАТЬ». От того, где должна стоять пропущенная телеграфистом точка, зависит судьба осужденного.
Головоломки этого типа также имеют многочисленные арифметические аналоги. Взять хотя бы следующее неверное равенство:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 100.
Как сделать его верным, изменив «пунктуацию» в левой части (то есть расставив по-другому плюсы и минусы и, возможно, убрав или добавив пробелы между цифрами)? Одно из возможных решений, использующее только три знака, имеет вид:
123 − 45 − 67 + 89 = 100.
Другое решение потребовало больше плюсов и лишь один минус:
1 + 2 + 3 − 4 + 5 + 6 + 78 + 9 = 100.
Существует всего лишь девять решений:
123 − 45 − 67 + 89 = 100,
123 + 4 − 5 + 67 − 89 = 100,
123 + 45 − 67 + 8 − 9 = 100,
123 − 4 − 5 − 6 − 7 + 8 − 9 = 100,
12 − 3 − 4 + 5 − 6 + 7 + 89 = 100,
12 + 3 + 4 + 5 − 6 − 7 + 89 = 100,
1 + 23 − 4 + 5 + 6 + 78 − 9 = 100,
1 + 2 + 34 − 5 + 67 − 8 + 9 = 100,
12 + 3 − 4 + 5 + 67 + 8 + 9 = 100,
1 + 23 − 4 + 56 + 7 + 8 + 9 = 100,
1 + 2 + 3 − 4 + 5 + 6 + 78 + 9 = 100.
Ту же задачу можно поставить несколько иначе, если потребовать, чтобы цифры шли не в порядке возрастания, а в порядке убывания. Если исключить (как мы делали в предыдущей, задаче) случай, когда знак минус стоит перед первым числом, то задача допускает всего 15 решений:
98 − 76 + 54 + 3 + 21 = 100,
9 − 8 + 7 − 6 − 1 − 54 − 32 + 1 = 100,
98 − 7 − 6 − 5 − 4 + 3 + 21 = 100,
9 − 8 + 7 + 65 − 4 + 32 − 1 = 100,
9 − 8 + 76 − 5 + 4 + 3 + 21 = 100,
98 − 7 + 6 + 5 + 4 − 3 − 2 − 1 = 100,
98 + 7 − 6 + 5 − 4 + 3 − 2 − 1 = 100,
98 + 7 + 6 − 5 − 4 − 3 + 2 − 1 = 100,
98 + 7 − 6 + 5 − 4 − 3 + 2 + 1 = 100,
98 − 7 + 6 + 5 − 4 + 3 − 2 + 1 = 100,
98 − 7 + 6 − 5 + 4 + 3 + 2 − 1 = 100,
98 + 7 − 6 − 5 + 4 + 3 − 2 + 1 = 100,
98 − 7 − 6 + 5 + 4 + 3 + 2 + 1 = 100,
9 + 8 + 76 + 5 + 4 − 3 + 2 − 1 = 100,
9 + 8 + 76 + 5 − 4 + 3 + 2 + 1 = 100.
Если мы условимся ставить минус и перед первым числом, то появится 3 новых решения в том случае, когда цифры расположены в порядке убывания, и одно новое решение, когда цифры расположены в порядке возрастания:
− 9 + 8 + 76 + 5 − 4 + 3 + 21 = 100,
− 9 + 8 + 7 + 65 − 4 + 32 + 1 = 100,
− 9 − 8 + 76 − 5 + 43 + 2 + 1 = 100,
− 1 + 2 − 3 + 4 + 5 + 6 + 78 + 9 = 100.
Разумеется, знаки «пунктуации» не обязательно ограничивать плюсами и минусами, а сумму, стоящую в правой части равенства, числом 100. Сумма может быть равна, например, двум последним цифрам текущего года или любому другому числу, какое вам больше нравится.
Можете ли вы расставить, знаки так, чтобы левая часть «равенства»
1 − 2 − 3 + 4 − 5 + 6 = 5
действительно стала равно 9?
Ответ приведен в конце книги.
Загадочные знаки
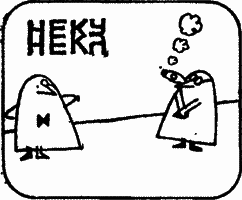
Проф. Слог. А теперь, мистер Рите, мы покажем вам три загадочные надписи. В каждой из них зашифровано какое-то слово. Раскройте тайный смысл любой из надписей, и вы получите сигары. Вот первая надпись. Каков ее тайный смысл?

Мистер Рите. Не знаю. Не могу сказать. А что в ней зашифровано?
Проф. Слог. Ваше имя — Неку. Таинственные символы получены при отражении букв от горизонтальной прямой, как от поверхности озера.

Проф. Слог. Может быть, разгадать эту надпись вам будет легче?

Слушая объяснения проф. Слога, мистер Рите только крутил головой.
Проф. Слог. Каждый символ был получен из соответствующей буквы при отражении от вертикальной прямой, проходящей слева от буквы. Не правда ли, все очень просто?
Мистер Рите. Мне это задание совсем не кажется простым.

Проф. Слог. Не будем спорить. Вот последнее ваше задание. У вас еще есть шанс получить сигары.
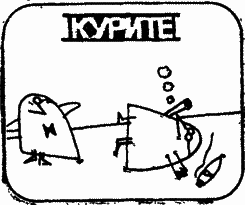
Мистер Рите не смог и с этим заданием справиться. Когда же проф. Слог провел по жирной черте над надписью и под ней, оказалось, что в ней было скрыто слово «курите».
В первой серии загадочных знаков буквы НЕКУ отражены от оси симметрии, проходящей через их основания. Заметим, что некоторые буквы при такой операции переходят в себя (например, буквы Н, Е и К, обладающие горизонтальной осью симметрии).
Во второй серии каждый загадочный знак получен при отражении букв РИТЕ относительно вертикальных осей симметрии. Заметим, что такие буквы, как Т и О (не входящая в имя и фамилию мистера Рите), при отражении относительно вертикальных прямых переходят в себя (они обладают вертикальной осью симметрии). Буква О, обладающая и вертикальной, и горизонтальной осью симметрии, не изменяется при отражениях в зеркале, поставленном, как перпендикулярно, так и параллельно строке. Возьмите зеркало и выясните, какой симметрией обладают все буквы алфавита, как строчные, так и прописные.
Можете ли вы придумать слово, которое бы не изменялось при отражении в зеркале, параллельном строке? Отражение в зеркале, поставленном параллельно строке, выдерживает в числе многих, например, слово «ОКНО». А существуют ли слова, способные выдержать отражение в зеркале, приставленном сбоку перпендикулярно строке? Да, одним из многочисленных примеров может служить слово «ТОПОТ».
Любая плоская фигура, обладающая по крайней мере одной осью симметрии, совместима со своим зеркальным отражением, хотя последнее может быть повернуто под некоторым углом. Любое геометрическое тело, обладающее плоскостью симметрии, также совместимо со своим зеркальным отражением. Глядя в зеркало, мы видим своих двойников именно потому, что наше тело обладает плоскостью симметрии, которая делит его от макушки до пят.