Есть идея! - Страница 13
Мы говорим о догадке потому, что формула, получаемая при помощи конечных разностей, может оказаться «ограниченно применимой» — порождать лишь часть членов бесконечной последовательности. Применимость формулы «конечно-разностного происхождения» ко всем без исключения членам числовой последовательности каждый раз необходимо доказывать особо. В случае круглого пирога такое доказательстве действительно существует. Его нетрудно найти, если воспользоваться методом математической индукции.
После этих замечаний, носящих сугубо предварительный характер, вы достаточно вооружены, чтобы смело вступить на неизведанную территорию и проложить по ней десятки увлекательных маршрутов в самых разных направлениях, многие из которых приводят к необычным числовым последовательностям, формулам и доказательствам методом математической индукции. Определить максимальное число частей, на которые можно разделить:
1) подковообразный пирог n прямыми;
2) головку сыра в форме шара или цилиндра n плоскими разрезами;
3) пирог n круговыми разрезами, проводимыми специальным ножом;
4) пирог, испеченный в форме кольца (с круглым отверстием посредине) n прямыми;
5) бублик (тор) n плоскими разрезами.
Во всех этих задачах предполагается, что разрезы проводятся одновременно. Как изменятся ответы, если будет разрешено проводить разрезы последовательно и после каждого разреза перекладывать образовавшиеся куски?
Невидимые размеры
В центре городского парка находится, круглая площадка для игр. Магистрат вознамерился устроить на этой площадке бассейн в форме ромба.
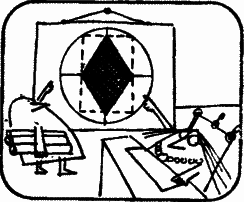
Мэр города Дорис Райт, рассмотрев представленные архитектором проекты, высказала свое мнение.
Мэр Райт. Мне нравится вот этот проект бассейна, облицованного красным кафелем. Какова длина каждой стороны ромба?

Вопрос мэра поставил в тупик архитектора Фрэнка Лойда Ронга.
Мистер Ронг. Сейчас прикину. Расстояние от A до B равно 5 м, а расстояние от B до C — 4 м. По этим данным можно найти длину стороны BD, например вычислить ее по теореме Пифагора.

Мистер Ронг приступил было к вычислениям, как вдруг достопочтенную миссис Райт осенило.
Мэр Райт. Есть идея! Длина стороны бассейна — ровно 9 м. Тут и считать нечего.
Мистер Ронг. Вы абсолютно правы!
Что позволило мэру и архитектору с такой легкостью найти длину стороны бассейна?
Миссис Райт заметила, что каждая сторона бассейна совпадает с диагональю некоего прямоугольника, другая диагональ которого равна радиусу круглой площадки для игр. Диагонали прямоугольника равны. Следовательно, длина стороны бассейна равна радиусу круглой площадки для игр. А поскольку этот радиус составляет 5 + 4 = 9 м, то и длина каждой стороны бассейна равна 9 м. Теорема Пифагора не понадобилась.
Вы сможете лучше оценить все остроумие догадки миссис Райт, если попытаетесь вычислить длину стороны бассейна более традиционным способом. Если вы захотите воспользоваться только теоремой Пифагора и подобием треугольников, то решение получится чрезмерно громоздким. Известная из планиметрии теорема о пересекающихся хордах, гласящая, что произведение длин отрезков, на которые точка пересечения делит хорды, одинаково для всех хорд, пересекающихся в данной точке, позволяет несколько сократить решение. Применяя эту теорему, вы числите высоту прямоугольного треугольника (составляющего четверть бассейна), равную √56. Затем по теореме Пифагора, зная два катета, вы найдете гипотенузу, равную 9 м.
С задачей о бассейне, так изящно решенной миссис Райт, тесно связана знаменитая задача о водяной лилии, встречающаяся в одном из произведений Лонгфелло. Когда стебель лилии стоит вертикально, цветок ее на 10 см возвышается над поверхностью озера. Если лилию оттянуть в сторону, не давая стеблю провиснуть, то цветок ее коснется воды в точке, отстоящей на 21 см от того места, в котором выходил из воды прямостоящий стебель. Какова глубина озера в том месте, где растет лилия?
Задачу Лонгфелло нетрудно решить, если начертить схему, изображенную на рис. 4. По существу эта схема ничем не отличается от проекта бассейна, представленного архитектором Ронгом. Требуется определить длину отрезка x. Как и задачу о длине стороны бассейна, задачу о лилии можно решить разными способами. Но если воспользоваться теоремой о пересекающихся хордах, то ответ получается особенно легко и быстро.

А вот еще одна замечательная задача о бассейне, трудная с виду, но легко решаемая, если сообщить, в чем ее изюминка. Дельфин находится у западного края круглого бассейна в точке A, проплывает по прямой 12 м и упирается «носом» в край бассейна в точке B. Повернувшись, он проплывает по прямой в другом направлении 5 м и снова касается края бассейна в точке C, диаметрально противоположной точке A. Какое расстояние пришлось бы преодолеть дельфину, если бы он из точки A поплыл прямо в точку C?
Задача о дельфине решается легко и просто, если воспользоваться теоремой о том, что любой вписанный угол, опирающийся на диаметр окружности, — прямой, и заметить, что угол ABC именно такой угол. Катеты прямоугольного треугольника ABC равны 5 м и 12 м. Следовательно, гипотенуза равна 13 м. Мораль всех этих задач ясна: во многих случаях геометрическую задачу можно решить до смешного просто, если вовремя вспомнить соответствующую теорему евклидовой геометрии.
Пасутся кони на другом поле

На заседании шахматного клуба мистер Бишоп предложил следующую задачу.
Мистер Бишоп. Как поменять позиции черных и белых коней за наименьшее число ходов?

Один из членов клуба сделал 2 первых хода так, как показано на диаграмме. Переставить белых коней в верхние углы доски, а черных — в нижние он сумел за 24 хода.

Другому члену клуба удалось решить задачу мистера Бишопа за 20 ходов.

Но никому не удавалось решить задачу менее чем за 18 ходов, пока не появилась Фанни Фиш.
Мисс Фиш. Есть идея! Я знаю, как решить задачу за 16 ходов, и могу доказать, что ее нельзя решить за меньшее число ходов.

Прежде чем приступить к объяснению, Фанни начертила диаграмму, на которой отрезками прямых изображены возможные ходы каждого коня.

Мисс Фиш. Представьте себе, что отрезки прямых — это нити, а восемь клеток нанизаны на них, как бусины, и их можно расположить по окружности.
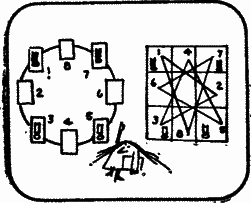
Мисс Фиш. Каждый ход на доске соответствует вполне определенному ходу на окружности. Чтобы поменять позиции коней, их необходимо переместить по окружности, двигая в одном направлении.

Мистер Бишоп. Вы совершенно правы, Фанни. Чтобы перейти на новую позицию, каждый из 4 коней должен совершить по 4 хода. Таким образом, задачу можно решить за 16 ходов, а более экономного решения не существует.