Экономическая статистика. Шпаргалка - Страница 4
где х — значение варьирующегося признака;
n – число единиц совокупности.
Базой для расчета взвешенной средней арифметической является обработанный цифровой материал, т. е. сгруппированные данные. Для таких данных используется формула средней арифметической взвешенной:
где х — значение варьирующегося признака;
m – веса, т. е. частоты, показывающие, сколько раз повторяется каждое значение признака в данной совокупности.
Формула получена путем взвешивания значений каждой варианты и деления суммы вариант на сумму весов. Формулы простой и взвешенной средней арифметической не эквивалентны друг другу.
Свойства средней арифметической:
1) алгебраическая сумма отклонений всех вариантов от средней арифметической равна нулю:
x = Σxm /Σm => x Σm = Σxm =>Σ(х-х)m = 0.
Это свойство используется для проверки правильности расчетов;
2) сумма квадратов отклонений вариант от их средней арифметической больше суммы квадратов отклонений вариант от любого другого числа, не равного средней арифметической:

где x ≠ a;
3) среднее алгебраическое суммы нескольких варьирующихся признаков равно сумме средних этих признаков:
k = x + y + z + …;
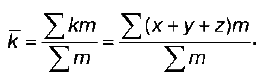
Это свойство позволяет определить сумму путем суммирования значений каких*либо признаков;
4) если все варианты (х) увеличить или уменьшить на какое-либо постоянное число (а), средняя (x) увеличится или уменьшится на то же самое число (y):
(х – а) = у;
x – a = y;
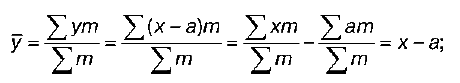
5) если все варианты (х) увеличить или уменьшить в одно и то же число раз (в), то средняя арифметическая увеличится или уменьшится в то же самое число раз:
если

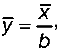
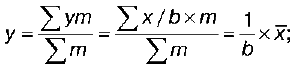
8. Средняя гармоническая, геометрическая, квадратическая, степенная
При решении задач расчет средней величины начинается с составления исходного отношения – логической словесной формулы средней. Она составляется на основе теоретического и логического анализа. Иногда среднюю арифметическую нельзя использовать. В этом случае в зависимости от ситуации применяется одна из трех форм средней.
Средняя гармоническая простая строится по формуле:

где n — число единиц совокупности или число вариантов;
х — значения варьирующегося признака.
Средняя гармоническая простая используется для несгруппированных данных.
Средняя гармоническая взвешенная строится по формуле:
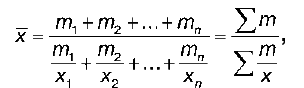
где х — значения варьирующего признака;
m — веса;
n — число единиц совокупности. Среднюю гармоническую взвешенную используют для сгруппированных данных, т. е. когда каждое значение х повторяется различное число раз.
Средняя квадратическая простая строится по формуле:
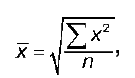
где n — число единиц совокупности или число вариантов; х — значения варьирующегося признака.
Средняя квадратическая простая используется для несгруппированных данных.
Средняя квадратическая взвешенная строится по формуле:
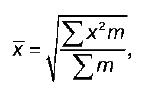
где m – веса;
х – значения варьирующего признака.
Среднюю квадратическую взвешенную используют для сгруппированных данных.
Данные формулы используются редко, в специальных расчетах.
Средняя геометрическая простая строится по формуле:

где n – число единиц совокупности или число вариантов;
х – значения варьирующегося признака. Средняя геометрическая простая используется для несгруппированных данных.
Средняя геометрическая взвешенная строится по формуле:

где х – значения варьирующего признака;
m – веса;
n – число единиц совокупности или число вариантов. Различные формулы средних величин можно объединить в одной формуле – формуле степенной средней:
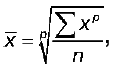
где р – порядок средней.
9. Медиана и мода. Асимметрия распределения
Медианой Ме называется варианта, которая делит ранжированный вариационный ряд на две равные части, из которых значение одной половины меньше медианы, а значения другой – больше медианы.
Медиана для несгруппированных данных при нечетном числе вариантов (n = 2k+ 1), определяется как Me = xk + 1, а при четном числе вариантов (n = 2k), медиана определяется по формуле:
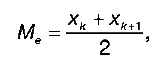
Медиана для сгруппированных данных рассчитывается по формуле:
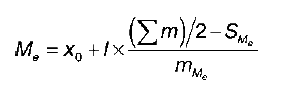
где х0 – это нижняя граница медианного интервала;
/– величина медианного интервала;
em / 2 – полусумма всех частот;
SMe – накопленная частота, предшествующая медианному интервалу;
mМе – частота медианного интервала.
Медиана рассчитывают наряду со средней величиной или вместо нее, когда в ряду данных присутствуют открытые или неравные интервалы. Это не влияет на точность медианы, однако, влияет на точность величины.
Модой М0 называется варианта, которая имеет наибольшую частоту по сравнению с другими частотами. В дискретно-вариационном ряду мода – это та варианта, которой соответствует наибольшая частота.
В интервальном вариационном ряду с равными интервалами моду определяют по формуле:
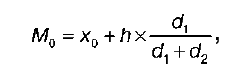
где х0 – это нижняя граница модального интервала;
h – величина модального интервала;
d1 – разность между частотами модального и предмодального интервалов;
d2 – разность между частотами модального и послемодального интервалов.
Мода рассчитывается в тех случаях, когда невозможно или нецелесообразно рассчитывать среднюю величину по обычным формулам.
Асимметрией распределения называется несоразмерность, т. е. нарушение соответствия в расположении частей одного целого относительно средней линии или центра. На графике асимметрия распределения определяется как вытянутость одной из ветвей распределения. Асимметрия распределения возникает в связи с различной частотой появления вариант больших или меньших моды (т. к. мода соответствует вершине распределения) под влиянием преобладающего действия определенных факторов. Таким образом, наличие асимметрии говорит о неустойчивости распределения совокупности в связи с преобладающим воздействием какой-либо группы факторов.