Досуги математические и не только. Книга 2 - Страница 2
Следовательно, ответ в первом примере будет 0,0080 с точностью до четвёртого знака; во втором примере ответ, с точностью до второго знака, будет 16211446,27.
§1. Делитель вида (10n ± 1) [3]
Год назад я обнаружил один любопытный [4] факт: если поставить «0» над разрядом единиц некоторого данного числа, которому случится быть кратным 9, и вычесть во всю длину, всякий раз ставя разность над следующей цифрой, то конечное вычитание даст 0 в остатке, а верхний ряд, по отбрасывании его конечного нуля, оказывается «частным-9» данного числа (то есть, частным от деления данного числа на 9).
Обнаружив этот факт, я тот час пришёл, по аналогии, к открытию того, что если поставить 0 под разрядом единиц некоторого данного числа, которому случится быть кратным 11, и действовать подобным образом, мы придём к подобному же результату.
В каждом случае я получал частное от деления столбиком более коротким и простым способом вычитания; но поскольку к этому результату можно было придти лишь в том (сравнительно редком) случае, когда данное число оказывалось точным кратным 9 или 11, это открытие виделось более любопытным, чем полезным.
Позднее я стал рассматривать случаи, когда данное число не было точным кратным. Я нашёл, что конечное вычитание при этом приносило некоторое число, иногда сразу являвшееся действительным остатком, получаемым от деления, но в любом случае дающее заготовку для нахождения такого остатка. Но поскольку оно не приносило частного (кроме как посредством некоторой весьма «экстравагантной» процедуры, значительно более длинной и трудоёмкой, чем подлинное деление), это открытие также не подлежало практическому применению.
Но совсем недавно мне пришло на ум выяснить, что будет, если после нахождения остатка поместить этот последний вместо того нуля над или под разрядом единиц, а затем вычесть как ранее. Меня поразило открытие того факта, что прежний результат повторился: конечное вычитание принесло 0 в остатке, а новая строка, по отбрасывании её разряда единиц, оказалась требуемым частным.
Существует, далее, более короткая процедура получения «остатка-9» и «остатка-11» некоторого данного числа, чем моё правило вычитания (процедура нахождения «остатка-11» есть ещё одно моё открытие). Усвоив её, я 28 сентября 1897 года довёл моё правило до завершения (я записал точную дату, поскольку это так приятно — быть открывателем новой и, как я надеюсь, практически полезной истины).
(1) Правило нахождения частного и остатка от деления данного числа на 9.
Чтобы найти «остаток-9», суммируем цифры; затем суммируем цифры результата и так далее, пока не останется единственная цифра. Если она будет меньше 9, это и будет искомый остаток; если это будет 9, искомый остаток равен нулю.
Чтобы найти «частное-9», проводим черту под нашим числом и ставим его «остаток-9» под разрядом единиц; затем вычитаем верхнее из нижнего, ставя разность под следующей цифрой, и так далее. Если крайняя левая цифра нашего числа меньше, чем 9, при её вычитании мы должны получить в остатке 0; если же она равна 9, мы должны получить в остатке 1, поставить в нижнюю строку да вычесть 1 заимствованное, что даёт в остатке 0. Теперь отчеркнём наш «остаток-9» на правом конце нижней строки, и оставшееся в ней будет «частным-9».
Примеры.
(2) Правило нахождения частного и остатка от деления данного числа на 11.
Чтобы найти «остаток-11», начинаем от разряда единиц и суммируем первую, третью и т. д. цифры, а также вторую, четвёртую и т. д.; находим «остаток-11» по разности этих сумм. Если первая сумма — большая, полученное таким образом число и будет искомым остатком; если же первая сумма — меньшая, искомый остаток будет разностью между полученным числом и числом «11»; если суммы равны, он есть 0.
Чтобы найти «частное-11», проводим черту под нашим числом и ставим его «остаток-11» под разрядом единиц; затем вычитаем <обычным порядком>, ставя разность под следующей цифрой, и так далее. Конечное вычитание должно дать в остатке 0. Теперь отчеркнём наш «остаток-11» на правом конце нижней строки, и оставшееся будет «частным-11».
Примеры.
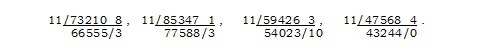
Эти новые Правила имеют ещё одно преимущество перед правилом подлинного деления, а именно что конечное вычитание обеспечивает нас критерием корректности результата: если оно не даёт в остатке 0, суммирование выполнено неверно, а если даёт, то либо суммирование выполнено верно, либо мы допустили две ошибки, — случай редкий.
Математикам не нужно и говорить, что правила, аналогичные вышеизложенным, с необходимостью будут действовать и для таких делителей, как 99, 101, 999, 1001 и т. д. Единственное видоизменение, которое необходимо будет внести — это разбить данное число на периоды по две или более цифр и обращаться с каждым таким периодом точно так же, как вышеизложенные правила требовали поступать с отдельными цифрами. Вот, для примера, целиком решение, требуемое для деления двух данных чисел на 999 и на 1001:

В первом из этих примеров число 2|437, написанное поверх, есть сумма по периодам. Поскольку она содержит 2 периода, поступаем с ней тем же образом, и итог, число 439, есть «остаток-999».
Во втором примере число 1|2269, написанное поверх, есть сумма первого и третьего периодов; число же 1383 есть сумма второго и четвёртого. Разность этих сумм равна 10886, чей «остаток-10001» равен 885 [5].
§2. Делитель вида (h10n ± k), в котором по крайней мере одно из двух чисел, h и k, больше 1 [6]
Способ, к которому мы приступаем теперь, приложим к трём отличным случаям:
(1) когда h > 1, k = 1;
(2) когда h = 1, k > 1;
(3) когда h > 1, k > 1.
При определённых ограничениях в отношении величин h, k и n, этот Способ окажется более короткой и более надёжной процедурой, чем обычное деление столбиком. Ограничения эти таковы: ни h, ни k не должны превышать 12, и когда k > 1, n не должно быть меньше, чем 3; вне этих ограничений нашему Способу присущи трудности, которые делают предпочтительной обычную процедуру.
При данном Способе требуются две раздельные процедуры — одна предназначена для случаев, когда h > 1, другая же для случаев, когда k > 1. Первая из этих процедур была, я полагаю, впервые открыта мной, а вторая — моим племянником, мистером Бертрамом Дж. Коллингвудом, который сообщил мне свой Способ, пригодный для делителей вида 10n – k.
В нижеследующем изложении я заменяю «10» буквой t [7].
Способ мистера Коллингвуда для делителей вида tn – k может быть изложен следующим образом:
«Чтобы разделить данное число на tn – k, отделяем в нём период из n цифр, начиная от разряда единиц, а затем записываем под ним увеличенное в k раз число, остающееся от первоначального при вычёркивании этого периода. Если это число содержит более чем n цифр, поступаем с ним тем же образом — и так далее, пока не будет достигнуто число, содержащее менее n цифр. Затем всё суммируем снизу доверху. Если последний период итога плюс увеличенная в k раз цифра, что была заимствована у него в процессе суммирования, будет меньше, чем наш делитель, то это и есть искомый остаток; оставшаяся часть итога есть искомое частное. Если этот [период] не меньше [делителя], то находим, какое количество раз он вмещает делитель, прибавляем это количество к частному и вычитаем это кратное делителя из остатка».