Большое, малое и человеческий разум - Страница 4

Размеры физических объектов на рисунке изменяются от 10^-15 м (характерный размер элементарных частиц) до 10²⁷ м (радиус наблюдаемой Вселенной, приблизительно соответствующий ее возрасту, умноженному на скорость света). Интересно оценить положение, которое на диаграмме занимаем мы, люди.

На шкале размеров мы находимся где-то в середине, будучи чрезвычайно крупными по отношению к длине Планка (и превышая на много порядков размеры элементарных частиц), но очень маленькими в масштабах всей Вселенной. С другой стороны, на временной шкале процессов длительность человеческой жизни выглядит совсем неплохо, и ее можно сопоставлять с возрастом Вселенной! Люди (и в особенности поэты) любят жаловаться на эфемерность человеческого существования, однако наше место на временной шкале вовсе не является жалким или ничтожным. Разумеется, нам следует помнить, что все сказанное относится к «логарифмической шкале», однако ее использование представляется совершенно оправданным при рассмотрении столь гигантских диапазонов значений. Говоря другими словами, число человеческих жизней, укладывающихся в возрасте Вселенной, намного меньше, чем число времен Планка (или даже времен жизни элементарных частиц), укладывающихся в продолжительность жизни человека. В сущности, мы являемся довольно стабильными структурами Вселенной. Что же касается пространственных масштабов, то мы действительно находимся где-то в середине шкалы, вследствие чего нам не дано воспринимать в непосредственных ощущениях ни очень большие, ни очень малые объекты окружающего нас физического мира.

Давайте рассмотрим, какие физические теории описывают объекты столь различных размеров. В схему рис. 1.5 я попытался «втиснуть» всю существующую физику. При этом мне, конечно, пришлось пожертвовать многими незначительными деталями (например, просто выкинуть из картины все уравнения и разделы наук!), однако, на мой взгляд, я сохранил фундаментальные теории.

Рис. 1.5.

Наиболее существенным обстоятельством является то, что в физике используются два совершенно разных подхода. Для описания поведения микрообъектов мы используем квантовую механику (я обозначил ее на рисунке словами «квантовый уровень»), о которой подробнее рассказано в гл. 2. Большинство людей полагают, что квантовая механика является странной, загадочной и недетерминистической теорией, но это неверно. На самом деле, если вы рассматриваете события на квантовом уровне, то квантовая теория является совершенно точной и детерминистической. Наиболее известным ее соотношением является уравнение Шредингера, которое определяет поведение физического состояния квантовой системы (его называют просто квантовым состоянием) и, безусловно, является совершенно точным и детерминистическим. Я использую букву U для обозначения всех расчетов или методов, связанных с квантовым уровнем рассмотрения. Неопределенность в квантовой механике возникает лишь тогда, когда вы осуществляете так называемое «измерение», требующее значительного «увеличения» масштаба события для перехода с квантового уровня на классический. Более подробно мы будем рассматривать эти проблемы в гл. 2.

При больших масштабах мы используем представления классической физики, которая является совершенно детерминистической. Она включает в себя законы механики Ньютона, законы Максвелла (позволяющие ввести в физику понятия электричества, магнетизма и света), две теории относительности Эйнштейна (специальную теорию относительности, описывающую движение тел при больших скоростях, и общую теорию относительности для систем с мощными гравитационными полями), причем все эти законы выполняются при больших расстояниях с исключительно высокой точностью.

Отмечу также, что на рис. 1.5 я использовал термин «вычислимость» для характеристики и квантовой, и классической физики. В первых двух главах это понятие практически не используется, но оно имеет важное значение для задач, обсуждаемых в гл. 3, где мы и рассмотрим проблему «вычислимости» более внимательно.

Настоящая глава посвящена в основном эйнштейновской теории относительности, ее характерным особенностям, исключительной точности, а также поразительной изящности и элегантности. Однако сначала необходимо рассказать хотя бы очень кратко о ньютоновской физике. Вскоре после того, как Эйнштейн разработал общую теорию относительности, Картан показал, что ньютоновская теория гравитации также позволяет ввести представление о едином пространстве-времени. Физическая картина в механике Галилея и Ньютона позволяет представить пространство-время введением глобальной (всемирной) временной координаты, после чего состояние системы может описываться просто набором последовательных диаграмм (рис. 1.6), в которых различным моментам времени соответствуют сечения четырехмерного пространства-времени. Каждому такому пространственному сечению (т. е. плоскости на рис. 1.6) соответствует обычное евклидово трехмерное пространство. Характерной особенностью ньютоновского пространства-времени является то, что все пространственные «сечения» существуют в нем как бы одновременно.

Рис. 1.6. Единое пространство-время в механике Галилея—Ньютона. Прямые линии соответствуют равномерно движущимся частицам.

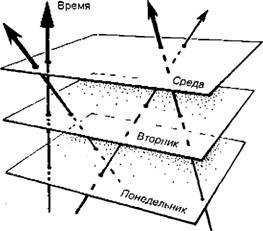
Таким образом, например, все события, происходящие в полночь понедельника, лежат в нижней горизонтальной плоскости диаграммы; все, что происходит в полночь вторника, — на следующей плоскости и т. д. Временные сечения по оси времени дают просто последовательность евклидовых пространств во времени. Все наблюдатели (независимо от их способа передвижения в пространстве-времени) фиксируют одни и те же события одновременно, поскольку они видят одни и те же «срезы», или «сечения», единого пространства-времени.

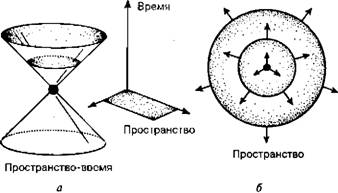
Совершенно иначе обстоят дела в специальной теории относительности Эйнштейна, где время и, соответственно, полная картина пространства-времени перестают быть универсальными величинами, как в физике Ньютона. Для демонстрации существенной разницы этих теорий нам необходимо прежде всего ввести одно из важнейших представлений теории относительности — так называемый световой конус.

Что такое световой конус? Представьте себе вспышку света в заданной точке пространства и в определенный момент времени (это и есть событие в пространстве-времени), после которой волны начинают распространяться со скоростью света, передавая сигнал о событии. В пространственных координатах фронт распространения имеет вид сферы, расширяющейся со скоростью света (рис. 1.7, б), однако в полной системе координат (пространство-время) мы получим значительно более сложную картину (рис. 1.7, а), в которой будут учитываться горизонтальные смещения, соответствующие сдвигам на рис. 1.6. К сожалению, изображение на рис. 1.7, а является всего лишь двумерным (плоскость рисунка), поскольку мы пользуемся всего лишь тремя измерениями для изображения четырехмерного пространства-времени. Поэтому нам приходится изображать вспышку света точкой в начале координат (событие), а затем — окружностями на горизонтальных сечениях, отражающими реальное движение лучей света (волн) через пространство. При этом движение световых лучей образует в пространстве-времени конус, верхняя часть которого описывает историю «вспышки» движением световых лучей в будущее пространство-время. С другой стороны, нижняя часть конуса соответствует приходу световых лучей из прошлого в точку вспышки (эту часть диаграммы обычно называют световым конусом прошлого). Наблюдатель получает всю информацию от световых лучей, распространяющихся по поверхности конуса!

Рис. 1.7. Распространение световой вспышки в пространстве-времени (а) и пространстве (б).