Большое, малое и человеческий разум - Страница 19
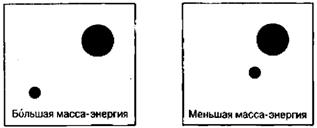
В общей теории относительности масса и энергия представляют собой довольно необычные величины. Прежде всего, масса эквивалентна энергии (деленной на квадрат скорости света) и, следовательно, энергия гравитационного потенциала вносит в массу свой вклад (причем отрицательный!). Соответственно, если два массивных объекта достаточно удалены друг от друга, то система в целом оказывается несколько массивнее, чем та же система с более близко расположенными объектами (рис. 2.21). Хотя плотность энергии-массы (измеряемой в единицах тензора энергии-импульса) равна нулю лишь внутри объема массивных объектов, а энергия каждого из них очень слабо зависит от другого, тем не менее некоторая разница в полной энергии двух систем, показанных на рис. 2.21, должна существовать. Полная энергия является нелокальной характеристикой, т.е. в общей теории относительности есть что-то принципиально нелокальное, связанное с энергией. Именно этим объясняется знаменитый эффект поведения двойных пульсаров, о котором я упоминал в гл. 1 (гравитационные волны уносят из системы положительную энергию и массу, однако энергия сохраняется нелокально за счет внешнего пространства). Вообще говоря, гравитационные волны представляют собой какой-то странный объект, ускользающий от наблюдателя. Мне кажется, что мы могли бы легко избавиться от всех ужасных проблем, связанных с поведением энергии при редукции вектора состояний, если бы нашли какой-то разумный метод объединения квантовой механики с общей теорией относительности. Проблема заключается в том, что при суперпозиции мы должны учитывать и гравитационный вклад состояний, однако никто не представляет, какой смысл имеет локальный вклад гравитации в энергию системы, вследствие чего и возникает существенная неопределенность в величине гравитационной энергии (эта неопределенность по порядку величины совпадает с предложенным выше значением Е). Именно с такой ситуацией мы сталкиваемся при рассмотрении процессов распада частиц. Неопределенность в энергии-массе нестабильных частиц обычно оказывается связанной с их временем жизни.
Рис. 2.21. Полная масса-энергия гравитирующей системы с учетом различной локализации масс.
Вопрос о явных или очевидных временных масштабах очень важен для рассматриваемых нами проблем, и я еще вернусь к нему в гл. 3. Каковы времена распада для реальных систем и какие пространственно-временные суперпозиции этому соответствуют? Считается, например, что время жизни протона (который условно можно считать просто твердым шариком) составляет несколько миллионов лет (оценка представляется весьма разумной, поскольку экспериментально распад одиночных протонов никогда не наблюдался). Для капельки воды время распада может составлять несколько часов (при радиусе ~10-5 см), одну двадцатую секунды (при радиусе ~10-4 см) или одну миллионную долю секунды (при радиусе ~10-3 см). Эти цифры наглядно показывают связь между масштабами и характером физических явлений.
Существует еще одно довольно важное обстоятельство, которое следует упомянуть. Ранее я немного подшучивал над сторонниками подхода FАРР (квантовая механика для всех практических целей), однако в этом подходе содержится и очень важный аспект, а именно: учет окружения, о котором я пока почти ничего не говорил. В реальных ситуациях учет окружения существенно важен для рассматриваемых нами задач. В сущности, мы не имеем права говорить просто «шар здесь» или «шар там», а должны каждый раз говорить о суперпозиции типа «этот шар плюс окружение» или «другой шар плюс его окружение» и т. д. Кроме того, необходимо очень внимательно проверять, связаны ли основные наблюдаемые эффекты с движением именно шаров и других тел или с их окружением. Если какая-то проблема связана с окружением, то наблюдаемый эффект будет случайным, а его описание будет иметь привычный вид. Однако если система достаточно изолированна и ролью окружения можно пренебречь, то в поведении системы, возможно, проявится нечто выходящее за рамки обычной квантовой механики. Было бы очень интересно предложить какие-либо разумные эксперименты этого типа (у меня имеются некоторые идеи на этот счет), которые доказали бы справедливость предлагаемой схемы или, наоборот, продемонстрировали, что привычные квантовые эффекты в этих условиях сохраняются, и мы действительно должны всерьез рассматривать существование суперпозиции состояний таких шаров (или, если угодно, котов).
На рис. 2.22 я попытался обобщить все приведенные выше рассуждения и свести их в некоторую схему. Для этого я расположил различные фундаментальные физические теории в вершинах некоторого абстрактного куба с несколько деформированными гранями (чуть ниже я поясню, что заставило меня использовать такой непривычный художественный прием). Три измерения этого куба соответствуют трем основным физическим константам: гравитационной постоянной G (горизонтальная ось), обратной скорости света с-1 (поперечная ось) и постоянной Дирака-Планка ћ (вертикальная ось, направленная вниз). В привычных нам единицах все упомянутые константы очень малы и их можно приравнять нулю при любых разумных приближениях. При равенстве нулю всех трех констант мы имеем картину мира, которую я называю физикой Галилея (верхний левый угол рисунка). Введение отличной от нуля гравитационной постоянной приводит нас вдоль горизонтальной оси к ньютоновской теории гравитации (геометрическое определение пространства-времени для этой теории было дано позднее Картаном). И наконец, использование неравной нулю величины с-1 приводит нас к специальной теории относительности в формулировке Пуанкаре-Эйнштейна-Минковского. Верхнюю «грань» нашего деформированного куба можно «достроить», считая отличными от нуля оба указанных выше коэффициента, что приводит нас к общей теории относительности Эйнштейна. Однако такое обобщение никак нельзя признать «честным», и поэтому я на рисунке изобразил соответствующую вершину куба несколько деформированной. Считая величину ћ отличной от нуля (но полагая при этом G = с-1 = 0), мы получаем обычную квантовую механику. Используя уже менее ясные варианты обобщения и вводя отличную от нуля величину с-1, мы можем получить квантовую теорию поля и замкнуть левую грань куба (она тоже немного искажена, чтобы подчеркнуть недостаток «прямоты» и ясности используемой методики).
Рис. 2.22.
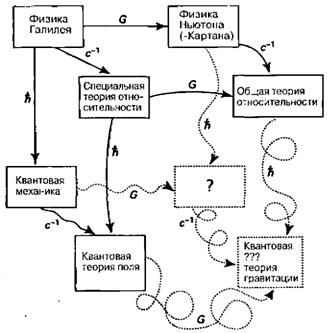
Мы не можем завершить построение указанного куба и получить общую картину связи различных теорий, так как принципы теории гравитации и квантовой механики существенно противоречат друг другу. Это противоречие проявляется даже в случае ньютоновской теории гравитации (где подразумевается, что с-1 = 0), если мы попытаемся получить соответствующую (картановскую) геометрию, в которой мог бы выполняться эйнштейновский принцип эквивалентности (напомню, что в соответствии с этим принципом постоянные гравитационные поля нельзя получить в ускоренных системах). На это обстоятельство указал мне Джой Кристиан, который также увлекался построениями типа рис. 2.22. Однако пока у нас нет никакой возможности объединения квантовой механики и ньютоновской гравитации (объединения, в котором эйнштейновский принцип эквивалентности будет учитываться совершенно строго, как в классической геометрической теории Картана), вследствие чего, по моему глубокому убеждению, мы должны искать пути такого объединения, пользуясь эффектом редукции квантовых состояний, что соответствует в основных чертах идеям теории OR, о которой я говорил в начале главы. Картина такого объединения пока еще очень туманна, и поэтому передняя грань куба (в отличие от задней!) пока выглядит совершенно бесформенной. Полная теория, в которой все три основные константы (ћ, G и с-1) не равны нулю и которая позволит нам правильно замкнуть грани предлагаемого «куба», должна включать в себя изящные и сложные математические схемы, которые нам еще предстоит разработать.