Бесчисленное поддается подсчету. Кантор. Бесконечность в математике - Страница 7
Целые числа также являются рациональными, например 3/1 = 3 и 0/1 = 0 (выражение 0/0 не представляет никакого рационального числа, как и 1/0, 2/0, 3/0...). Следовательно, мы можем доказать, что множество рациональных чисел включает в себя и множество целых чисел, которое, в свою очередь, включает множество натуральных чисел. И тем не менее между множеством рациональных чисел, с одной стороны, и множеством натуральных и целых чисел, с другой, есть фундаментальное различие. Чтобы объяснить его суть, нам понадобится числовая ось. Это прямая (ее можно представить себе как потенциально, так и как актуально бесконечную), на которой отмечены числа. Сначала выберем произвольную точку и отметим на ней число 0, а потом еще одну, на которой отметим 1.
Каждая из этих точек на самом деле является математической, то есть не обладает длиной, но в данном случае, чтобы сделать их видимыми, мы обозначим их маленькими окружностями.
Выбор места для точек 0 и 1 совершенно произволен, но, сделав его, мы обусловим расположение остальных чисел. Расстояние между 0 и 1 должно равняться расстоянию между 1 и 2, а также расстоянию между 2 и 3 и так далее. То же справедливо и для отрицательных чисел.


Георг Кантор в 1870 году по прибытии в Галльский университет.

Университет в Галле, приблизительно 1936 год.

Портрет Рихарда Дедекинда. Генрих Кенигсдорф, 1927 год.

Портрет Карла Теодора Вильгельма Вейерштрасса. Конрад Фер.
Немецкий математик Давид Гильберт (1862-1943) придумал задачу, в которой упрощенно излагается одно из следствий теории Кантора. Представим себе отель, в котором есть бесконечное количество комнат, обозначенных номерами 1, 2, 3, 4, 5 и так далее. В каждом номере есть постояльцы, которых мы для удобства так же обозначим числами 1, 2, 3, 4, 5 и так далее. Однажды в отель приезжает новый гость, назовем его Господином 0, но все номера заняты, а по правилам отеля двое людей не могут занимать один номер. Господин 0 уже собирается уходить, когда ему предлагают такой вариант: он поселится в номере 1, гость 1 — в номере 2, гость 2 — в номере 3 и так далее. Таким образом, Господин 0 сможет остановиться в отеле, и никто не останется без комнаты.

На языке математики эта история доказывает, что множество чисел 0, 1, 2, 3,4,... эквивалентно множеству чисел 1, 2, 3, 4, 5,... То есть любое бесконечное множество, к которому добавляется новый элемент, эквивалентно изначальному множеству.
Положение каждого рационального числа также строго определено. Если мы разделим отрезок между 0 и 1 на шесть равных частей, первой точке после 0 будет соответствовать число 1/6, второй — 2/6 (обратим внимание, что 2/6 = 1/3), третьей — 3/6 (то есть 1/2) и так далее.

Существуют ли рациональные числа между 1/3 и 1/2? Да, так как, например, есть их среднее арифметическое, 5/12. А между 1/3 и 5/12? Тоже: их средним арифметическим будет 3/8. Таким образом, как бы близко друг к другу ни располагались два рациональных числа, между ними всегда будут другие рациональные числа.
Из этого следует, что любой отрезок числовой оси, каким бы маленьким он ни был, всегда будет содержать бесконечное количество рациональных чисел. В этом и заключается различие между рациональными и целыми числами. Разумеется, ни натуральные, ни целые числа этим свойством не обладают. Следовательно, мы можем утверждать, что рациональных чисел на числовой оси больше, чем натуральных, но все-таки между ними есть взаимно однозначное соответствие.
Чтобы объяснить, как оно возникает (и открыл его Кантор), отметим на оси дроби, полученные с помощью двух натуральных чисел. Сначала запишем единственную дробь, составляющие которой в сумме равны 2:1/1. Затем дроби, составляющие которых в сумме равны 3: 1/2 и 2/1. После дроби, составляющие которых в сумме равны 4:1/3 и 3/1, опуская дробь 2/2, так как 2/2 = 1/1, а ее мы уже отметили. Продолжим с дробями, составляющие которых в сумме дают 5, затем 6 и так далее, всегда опуская дроби, равные уже записанным. У нас получится ось, которая в начале выглядит следующим образом.

Если мы продолжим эту линию на достаточное расстояние, в конце концов на ней появится какое-то положительное рациональное число (мы представляем эту ось как потенциально бесконечную). Чтобы включить и другие рациональные числа, поставим в начале 0 и будем чередовать положительные и отрицательные числа:
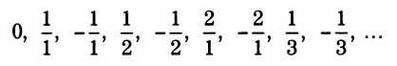
После этого, чтобы закончить соответствие, соотнесем 0 с первым числом оси, 1 — со вторым, 2-е третьим и так далее.

Таким образом, мы доказали, что между множествами натуральных и рациональных чисел есть взаимно однозначное соответствие.
Но Кантор в статье 1874 года, следуя совету Вейерштрасса, не упоминал об этих соответствиях (лишь намекнул), а также о кардинальных числах. Как тогда он мог утверждать, что некая группа чисел эквивалентна группе натуральных чисел? Для этого Кантор использовал понятие, которое стало одним из основных в его теориях: последовательность.
В последовательности всегда есть первое число, второе и так далее. Существуют последовательность нечетных натуральных чисел (1, 3, 5, 7, 9, 11, ...) и последовательность простых чисел (2, 3, 5, 7, 11,...). Последовательности могут иметь и конечное число членов, но мы рассмотрим только те из них, которые, как в предыдущих примерах, состоят из бесконечного количества не повторяющихся членов.
Заметим, что для установления взаимно однозначного соответствия между натуральными и целыми числами мы должны сначала представить их в виде последовательности: 0,1, -1, 2, -2, 3, -3,... То же самое необходимо для установления соответствия между натуральными и рациональными числами:
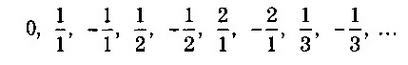
Следовательно, утверждение, что некое множество чисел эквивалентно множеству натуральных чисел, означает, что его члены могут быть представлены в виде последовательности.
Я бы с удовольствием вставил комментарий о фундаментальном различии между группами, но убрал его, следуя совету господина Вейерштрасса.
Георг Кантор в письме Рихарду Дедекинду 27 декабря 1873 года
Используя это следствие, Кантор не стал упоминать в своей статье ни об эквивалентности натуральным числам, ни об общем кардинальном числе, а просто рассмотрел возможность организации членов некоей группы в виде последовательности.
Теперь вернемся к числовой оси и предположим, что мы уже отметили числа 0 и 1. Исходя из этих отметок, позиции других чисел тоже строго определены. Будет ли ось полностью заполнена, если мы отметим на ней рациональные числа? Другими словами, можно ли записать все числа как соотношение двух целых чисел? Ответ на оба вопроса: нет. После того как мы нанесем на ось все рациональные числа, на ней все равно останутся точки, которым не будет соответствовать никакое число. Открытие иррациональных чисел приписывается Пифагору (VI век до н.э.), хотя, возможно, это был кто-то из его учеников. Иррациональные числа не могут быть представлены в виде соотношения целого и натурального числа, например √2-1,4142.... .. и π = 3,14159... Дополняют ось вещественные числа.