Анафем - Страница 198

Фраа,инак.

Халикаарнийский,относящийся к св. Халикаарну либо к какому-либо из орденов, восходящих к семантической группе. Халикаарнийцы воспринимаются как естественные противники проциан и фаанитов.

Халикаарн,светитель последних десятилетий эпохи Праксиса, вступивший в резкую полемику со своим современником Процем. Иногда называется св. Халикаарном Великим. В наиболее широком смысле рассматривается как лидер теорической школы, созданной тысячелетиями раньше Протесом и Феленом и продолженной после смерти X. его учеником Эвенедриком и семантической группой.

Хорошин,природное химическое соединение, которое при определённой концентрации в мозгу вызывает чувство, что всё в целом неплохо. Его уровень можно повысить искусственно, например, употреблением раданицы.

Хроника,летопись всех событий, больших и малых, происходящих в конценте либо матике. Тщательно ведётся и архивируется иерархами.

Хронобездна,в матической архитектуре пространство внутри часовой башни, где находится механизм часов и сопутствующего оборудования: циферблатов, боя и тому подобного.

Центенарий,инак, давший обет не выходить из матика и не иметь контактов с внешним миром до следующего столетнего аперта. Разг. «столетник».

Цепочка,генетический код живого организма. В различных контекстах может соответствовать понятиям «ген» либо «ДНК» на Земле.

Эвенедрик,ученик Халикаарна, продолживший его труды во время Реконструкции и участвовавший в создании семантической группы.

Эвенедриканцы,ранее ответвление халикаарнийцев.

Эдхар,св., член эвенедриканского ордена, основавший в 297 г. орден, а затем и концент, в котором жил до самой смерти. И орден, и концент впоследствии получили его имя. Полное название последнего «концент св. Э.», но в разговорной речи чаще используется сокращённый вариант «Э.».

Экба,вулканический остров в Море морей, на котором до катастрофического извержения –2621 г. стоял Орифенский храм.

Экстрамурос,мир за стенами матика; секулярный мир.

Эксы,слегка презрительный термин, используемый инаками по отношению к мирянам.

Элигер,актал, при котором фид избирает конкретный капитул в своём матике, а также избирается этим капитулом и, таким образом, перестаёт быть фидом. Обычно отмечается незадолго до двадцатилетия.

Эразмас,фраа концента св. Барито в XIV веке от РК, вместе с Утентиной основавший ветвь метатеорики, называемую сложным протесизмом. Так же его тёзка, фраа концента св. Эдхара в тридцать седьмом веке, рассказчик «Анафема».

Этреванические,см. отношения этреванические.

Эфрада,относительно процветающий и могущественный город-государство древнего мира, который в период своего Золотого века (приблизительно с –2600 по 2300 год) был приютом многих теоров, в том числе Фелена и Протеса. Место действия многих знаменитых диалогов, которые изучают, разыгрывают и заучивают наизусть фиды.

Приложение к «Анафему» Нила Стивенсона

— Давай договоримся, что каждая порция будет квадратом со стороной, равной ширине лопаточки. Отрежь уголок коврижки. Дат отрезал вот так:

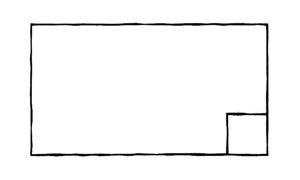
И разделил кусок на четыре порции того размера, о котором я говорил:

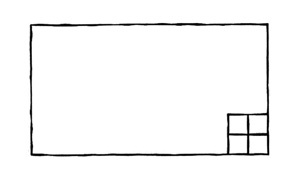
— Не могу поверить, что ты правда это делаешь, — пробормотал Арсибальт.

— У Фелена вышло… — буркнул я. — А теперь молчи и не мешай.

Я взглянул на Дата, ждущего указаний.

— Сколько порций у нас вышло?

— Четыре, — отвечал он, немного сбитый с толку элементарностью моего вопроса.

— Теперь: что, если ты отрежешь похожую фигуру, но со стороной в два раза больше? Чтобы каждая сторона была не в две единицы — две лопаточки — а…

— В четыре?

— Да. У нас уже есть четыре порции. Если ты удвоишь сторону фигуры, то скольких людей мы сможем накормить?

— Ну, дважды четыре — восемь.

— Я согласен, что дважды четыре — восемь. Давай проверим, что у тебя получится, — сказал я.

Дат начал резать.

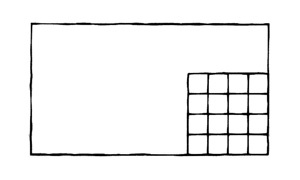
В середине процесса он понял свою ошибку и нахмурился, но я велел ему продолжать.

— Шестнадцать, — сказал Дат наконец. — У нас получилось шестнадцать порций. Не восемь.

— Подведём итог. Прямоугольная решётка со стороной в две единицы даёт нам сколько порций?

— Четыре.

— И ты только что мне сказал, что решётка со стороной в четыре единицы даёт нам шестнадцать. А если нам нужно всего восемь порций? Какой длины должна быть сторона квадрата?

— В три лопаточки? — осторожно спросил Дат. Затем он посмотрел на пирог и сосчитал. — Нет, так получится девять.

— Но мы уже ближе к цели. И вот существенный результат: ты не знаешь, как решить задачу, и осознаешь своё незнание.

У Дата брови поползли вверх.

— Это существенно?

— Для нас здесь — существенно.

Я забыл, каким был следующий шаг Фелена, когда тот объяснял эту задачку мальчику-рабу на Плоскости шесть тысячелетий назад, поэтому вынужден был обратиться за помощью к Ороло.

Затем я развернул коврижку нетронутым углом к Дату.

— Отрежь квадратный кусок на четыре порции. Отдельные порции можно не нарезать.

— А чертить на глазури можно? — спросил Дат.

— Если тебе так проще — черти.

С помощью Корд Дат изобразил такой квадрат:

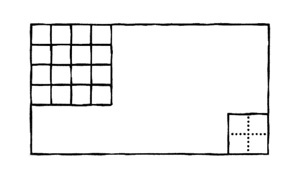
Отлично, — сказал я. — Я теперь добавь три таких же квадрата.

Продолжив уже проведённые линии и добавив новые, Дат получил следующую картину:

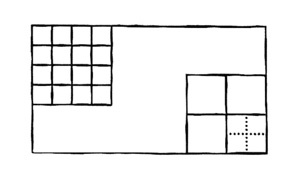
— Теперь напомни, сколько порций мы можем из этого сделать?

— Шестнадцать.

— Отлично. А теперь смотри на квадрат в правом нижнем углу.

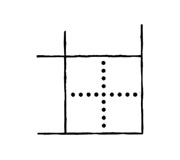
— Можешь ли ты одним надрезом разделить его ровно пополам? Дат уже приготовился провести лопаточкой по пунктирной линии, но я покачал головой.

— Арсибальт очень трепетно относится к этой коврижке и хочет быть уверен, что никому не достанется кусок больше, чем у него.

— Спасибо тебе огромное, мудрый Фелен, — вставил Арсибальт.

Я сделал вид, будто не слышу.

— Можешь ты сделать один надрез так, чтобы Арсибальт точно остался доволен? Кускам не обязательно быть квадратными. Годятся и другие фигуры — например, треугольники.

После моей подсказки Дат сделал такой разрез:

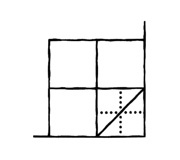
— Ну, теперь остальные так же, — сказал я.

Дат разрезал.

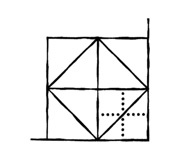
— Когда ты сделал первый диагональный разрез, ты разделил квадрат точно пополам, верно?

— Верно.

— И то же самое относится к трём другим диагональным разрезам и трём остальным квадратам?

— Конечно.

— Допустим, я повернул противень и ты посмотришь на него так:

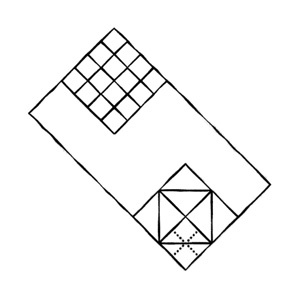
Какую фигуру ты видишь в середине?

— Квадрат.

— И сколько кусков коврижки в этом квадрате?

— Четыре.

— Он составлен из четырёх треугольников, верно?

— Ага.

— Каждый из треугольников — половина квадрата, верно?

— Верно.

— Сколько порций в маленьком квадрате?

— Четыре.

— Значит, в каждом треугольнике сколько порций?

— Две.

— А в квадрате, состоящем из четырёх таких треугольников?..

— Восемь порций. — Тут до него дошло: — Это та задача, которую мы пытались решить раньше!

— Мы всё время её решали, — поправил я. — Просто нам потребовалось несколько минут. А теперь отрежь нам, пожалуйста, восемь порций.